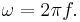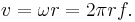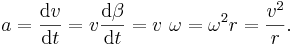Rotationshastighet
Från Rilpedia
Rotationshastighet eller vinkelhastighet är ett mått på hur snabbt vinkeln ökar när ett föremål vrider sig runt en rotationsaxel. Om en punkt på det roterande föremålet ligger på avståndet r från rotationsaxeln och rör sig med hastigheten v, kan rotationshastigheten beräknas som v/r.
SI-enhet för vinkelhastighet är radianer per sekund. Ofta används den grekiska bokstaven ω för att beteckna storheter för vinkelhastighet.
Andra mått på rotationshastighet är varvtal och frekvens, antalet varv som en ökande vinkel gör per tidsenhet. Varvtal anges ofta per minut (RPM, rotations per minute) medan frekvens normalt anges per sekund (hertz, cycles per second).
Några enkla samband
Multipliceras vinkelhastigheten med den tid rotationen pågått, ω•t, fås den vinkel som uppnåtts vid denna tid. Vinkeln kan då vara många varv stor. Eftersom ett varv är 2π radianer, kan vinkelhastigheten ω räknas om till antalet varv per tidsenhet, vilket är detsamma som frekvensen f. Sambandet är:
Exempel: Frekvensen f = 5 Hz motsvarar vinkelhastigheten ω = 2π rad • 5 Hz ≈ 31,4 rad/s. Efter 10 sekunder har föremålet roterat ω•t ≈ 31,4 rad/s • 10s = 314 rad, vilket hade blivit precis 50 varv om vi kunnat ta med alla decimalerna på π.
En punkts hastighet v är direkt proportionell mot vinkelhastigheten ω och avståndet r till rotationsaxeln :
När vinkelhastigheten är konstant, talar man om uniform cirkulär rörelse. En punkt färdas då med konstant fart över en cirkelbana, men dess riktning ändras, och punkten har hela tiden en acceleration mot cirkelns mittpunkt. Figuren till höger visar att dess storlek är proportionell mot hastigheten och mot ändringshastigheten i vinkeln dβ/dt. Centripetalaccelerationen ges därför av
Tillämpningar
I klassisk mekanik används rotationshastigheten i följande exempel.
- En satellit eller en planet som roterar i en cirkulär bana runt sitt centrum. Satelliten rör sig då med konstant rotationshastighet.
- En kropp roterar kring en fast axel utan påverkan av andra yttre krafter. Varje punkt roterar då med konstant rotationshastighet relativt axeln.
- Om rotationsaxeln inte är fast, kan rörelserna bli komplicerade, med precession och nutation av rotationsaxeln. För ett fritt föremål går rotationsaxlar alltid genom kroppens tyngdpunkt. Rörelseekvationerna är lösbara om föremålet är en stel kropp.
Rotationshastigheten är en pseudovektor.