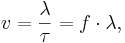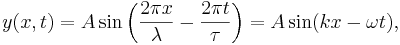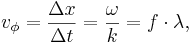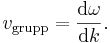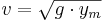Våghastighet

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Våghastighet eller utbredningshastighet är den hastighet som vågor (vågdalar, vågberg förtätningar och förtunningar) rör sig med. Våghastigheten varierar mycket beroende på vilket medium som vågorna färdas i, se vidare ljudhastighet, ljushastighet och vattenvågor.

En löpande våg

Det finns ett samband mellan våghastighet, våglängd och period eller frekvens. Under en oscillationsperiod τ utbreder vågen sig öven en våglängd λ. Våghastigheten v blir därför:

v = \frac{\lambda}{\tau} = f \cdot \lambda,

där f = 1/τ är frekvens.

Mera noggrant uttryckt är detta ett uttryck för vågens fashastighet. För ljus i genomskinliga ämnen är fashastigheten lika med c/n, där c är ljusets hastighet i vakuum och n är ämnets brytningsindex. Om fashastighet beror på frekvens, finns det dispersion. Fasthastighet är då inte lika med grupphastighet eller med signalhastighet.

Fashastighet

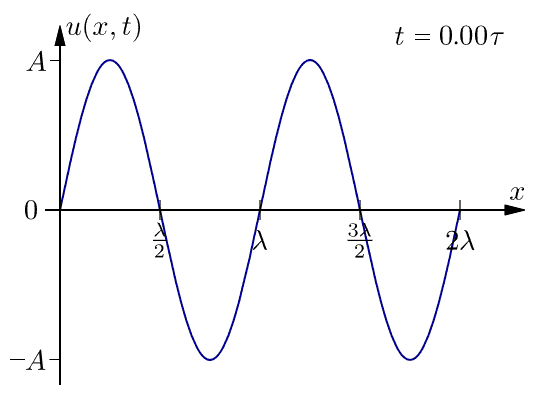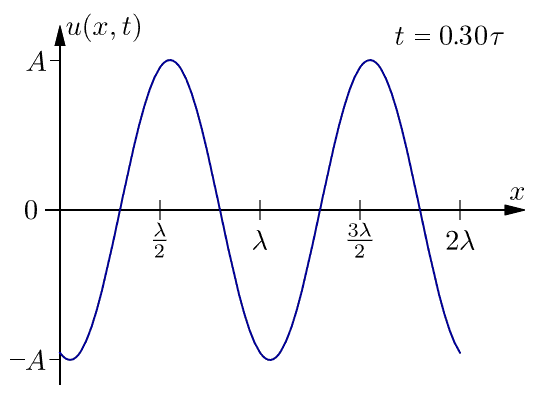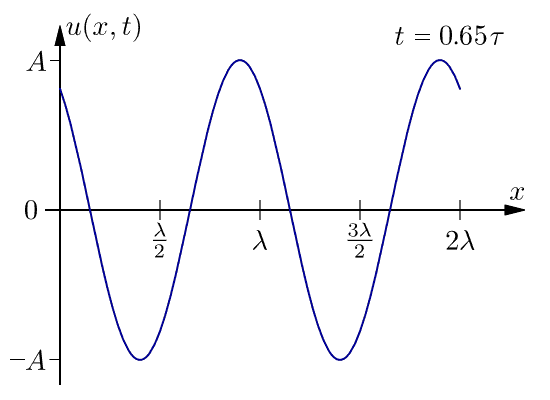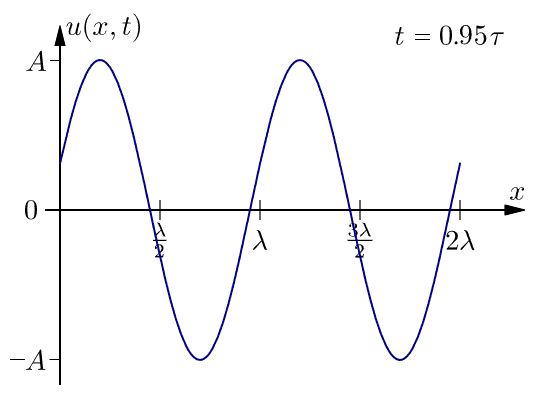
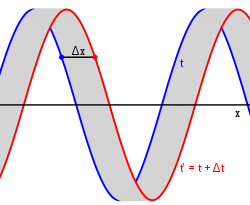
En våg som funktion av x vid två tidpunkter. En markerad punkt med bestämd fas ligger vid den senare tiden vid större x. Fashastigheten är Δx/Δt.

Termen fashastighet är mer noggrant definierad än väghastighet. Man betraktar en punkt på en oändligt lång sinusvåg med en bestämd fas vid en tidpunt t, se figur. En kort tid Δt senare har en annan punkt denna fas. Fashastigheten är skillnaden i position av dessa två punkter delad med tidsskillnaden.

Matematiskt kan man beskriva en löpande våg i en dimension med uttrycket

y(x,t) =A \sin\left(\frac{2\pi x}{\lambda} - \frac{2\pi t}{\tau}\right)= A\sin(kx -\omega t),

där k=2π/λ är det cirkulära vågtalet och ω=2πf är vinkelfrekvensen. Punkten har samma fasfaktor kx-ωt vid de båda tidpunkterna. Genom subtraktion får man:

v_\phi = \frac{\Delta x}{\Delta t}= \frac{\omega}{k} = f \cdot \lambda,

i överensstämmelse med resultatet ovan. Grupphastigheten är dock

v_\mathrm{grupp} = \frac{\mathrm{d}\omega}{\mathrm{d}k}.

Gravitationsvåghastigheten inom kanalströmning

Inom kanalströmningen är förhållandet mellan gravitationsvåghastigheten och vattnets medelhastighet (Froudes tal) direkt avgörande för vilket strömningstillstånd som erhålles. Här definieras gravitationsvåghastigheten enligt följande:

v = \sqrt {g \cdot y_m}

där

v = Gravitationsvåghastighet (m/s)

g = Tyngdaccelerationen (9,82 m/s2)

ym = Vattnets medeldjup (m)


Se även

Hämtad från "https://sv.rilpedia.org/wiki/V%C3%A5ghastighet"
Personliga verktyg
På andra språk