Thomaes funktion

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Thomaes funktion på intervallet

(0,1)

Thomaes function, Riemannfunktionen eller i engelsktalande länder popcornfunktionen är en funktion som är kontinuerlig i alla irrationella punkter och diskontinuerlig i alla rationella.

Funktionen definition är

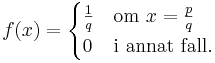$f(x)=\begin{cases} \frac{1}{q} & \text{om }x=\frac{p}{q}\\ 0 & \text{i annat fall}. \end{cases}$ ,

där $p$ och $q$ är heltal och bråket $p / q$ är förkortat så mycket som möjligt.

Kontinuitet i irrationella punkter

Låt $x$ vara ett irrationellt tal och $n$ ett heltal. Vi kan definera

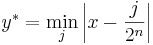$y^* = \min_j \left| x - \frac{j}{2^n} \right|$ .

Då är för $ε = 2 - n$

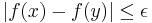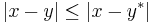$|f(x) - f(y)| \le \epsilon$ om $|x-y| \le |x-y^*|$ .

Detta visar att $f$ är kontinuerlig i $x$ .

Diskontinuitet i rationella punkter

Om $x = p / q$ finns det för varje $δ > 0$ ett (irrationellt) $y$ så att

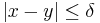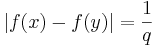$|x-y| \le \delta$ men $|f(x)-f(y)| = \frac{1}{q}$ .

Detta visar att $f$ är diskontinuerlig i $x$ .

Se även

Dirichlets funktion

Thomaes funktion

Från Rilpedia

Kontinuitet i irrationella punkter

Diskontinuitet i rationella punkter

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk