Sturm-Liouvilles ekvation
Från Rilpedia
(Omdirigerad från Sturm-Liouville-ekvation)
Sturm-Liouvilles ekvation är en ordinär differentialekvation av andra graden:
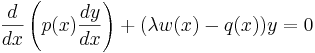
Där λ är en konstant, p(x), q(x) och w(x) är kända funktion, där w(x) kallas antingen densitetsfunktionen eller viktningsfunktionen. Lösningen (som fås med lämpliga randvillkor) av λ är egenvärden, och de motsvarande uλ(x) egenfunktioner. Lösningarna till denna ekvation uppfyller - tillsammans med vissa randvillkor och krav på w ,p och q - viktiga matematiska egenskaper.
Exempel
En form av Sturm-Liouvilles ekvation som ofta förekommer inom t.ex. kvantmekanik ("partikel i låda") är:
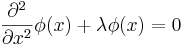
som har allmän lösning:
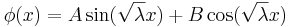
Med randvillkor φ(0) = φ(L) = 0 fås de ytterligare villkoren 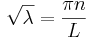 för något heltal n, och B=0
för något heltal n, och B=0



