Spektroskopi
Från Rilpedia
Spektroskopi är samlingsnamnet för experimentella metoder där man använder en del av det elektromagnetiska spektrumet för att undersöka materia, dvs. grundämnen eller föreningar. I sin vidare mening kan man också inkludera metoder där partiklar såsom elektroner, neutroner eller atomer används som informationsbärare.
Ordet spektroskopi anger ordagrant att man tittar på ett spektrum. Historiskt har de spektroskopiska metoderna utvecklats ur iakttagelser av spektra av det slag som man får när ljuset från till exempel solen får passera ett prisma. Om det även passerat genom en gas kan man iaktta mörka band eller linjer i spektret, beroende på att gasens atomer eller molekyler absorberat ljus av vissa våglängder. Sådana absorptionsband, liksom ljusa emissionsband, kan också iakttas i spektrum från stjärnor. Jämförelse mellan stjärnspektra och laboratoriespektra har sedan 1800-talet betytt enormt för förståelsen av världsrymden. I och med kvantmekanikens utveckling har spektroskopiska metoder bringat klarhet i atomers egenskaper. Spektroskopi omfattar idag inte bara det synliga spektret utan alla mätbara våglängdsområden. När man inte bara iakttar att det finns ett mörkt eller ljust band vid en viss våglängd utan man mäter både våglängd och intensitet talar man om spektrometri. Det gemensamma för all spektrometri är en intensitet som en funktion av en våglängd eller frekvens. En graf som visar detta funktionssamband kallas spektrogram. Med undantag av masspektrometri har termen spektrometri dock inte slagit igenom helt och hållet, och vissa metoder med vilka man nog kan mäta en signals intensitet, till exempel NMR-spektroskopi, kallas alltjämt "spektroskopi".
Man kan grovt dela in spektroskopi i absorptions- och emissionsspektroskopi. I det första tar en atom upp ljus och i det senare avger atomer ljus. För att fullständigt kunna förklara denna process måste den behandlas inom kvantmekaniken. Inom kvantmekaniken finns förklaringen för varför elektroner i atomer bara tillåts inneha vissa bestämda, det vill säga diskreta, energivärden (en bildlig jämförelse skulle vara till exempel en stjärna som endast kan ha planetbanor med vissa radier).
När elektroner hoppar mellan dessa energitillstånd ("banor" eller elektronskal) avges eller tas det upp ett ljuskvantum (en foton) med en energi som motsvarar skillnaden i elektronens energi i dessa tillstånd, detta kallas excitation. Man kan visa i kvantmekaniken att en fotons energi motsvarar en viss våglängd: 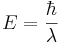 , där
, där 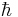 är Diracs konstant och λ är ljusets våglängd.
är Diracs konstant och λ är ljusets våglängd.
Ett fullständigt spektrum motsvarar alltså alla möjliga skillnader mellan elektrontillstånd i en atom. Varje grundämne har en alldeles egen uppsättning av elektrontillstånd och därigenom har det ett unikt spektrum.
Spektra av föreningar (molekyler eller fasta kroppar) kan vara mer diffusa. Detta händer då allt fler atomer av samma slag sammankommer och deltar i bindningen. Då minskas energiskillnaden mellan elektrontillstånden tills de flyter ihop och bildar band. Detta innebär att också skillnaderna mellan föreningarnas respektive spektra minskar när sådana tillstånd förekommer. Detta händer oftast i optiska området som involverar synligt ljus. I röntgenområdet deltar dock elektrontillstånd med diskreta väl skilda energier som lämpar sig bättre för undersökningar där mer än bara ett fåtal atomer är inblandade.
Molekyler kan rotera och vibrera vilket påverkar de krafter som verkar på elektronerna och därför också vilka banor de kan gå i.
Den påverkan rotationen har på energibanorna beskrivs av formeln:
![E_r=\hbar c\left [ BJ \left (J+1 \right ) -DJ^2 \left (J+1 \right ) ^2 \right ] \quad](/w/images/sv.rilpedia.org/math/d/a/9/da9cf5f49d1e9262c16d0fd4d20b8613.png)
där, 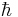 är Plancks konstant, c är ljusets hastighet, B är en rotationskonstant, angiven nedan och D är en korrektionsterm orsakad av centrifugaleffekter.
är Plancks konstant, c är ljusets hastighet, B är en rotationskonstant, angiven nedan och D är en korrektionsterm orsakad av centrifugaleffekter.
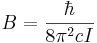
där I står för tröghetsmomentet.
Den påverkan vibrationen har på energibanorna beskrivs av formeln:
![E_r=\hbar c\left [ \omega _e \left (\nu+\frac{1}{2} \right ) - \omega _e\chi e \left (\nu+\frac{1}{2} \right ) ^2 + \omega _ey_e \left (\nu+\frac{1}{2} \right )^3 + ... \right ] \quad](/w/images/sv.rilpedia.org/math/6/b/b/6bbaeaf50721dace8c4084bb3e493ac1.png)
ν är vibrationskvanttalet, ωe = ν / c, medan χe och ye är konstanter.
Den första parentesen utgår från vibration baserad på en harmonisk oscillator, medan övriga parenteser sedan tar hänsyn till de anharmoniska delarna.
Exempel på olika spektroskopitekniker
- Kärnmagnetisk resonansspektroskopi (NMR-spektroskopi)
- Masspektrometri
- Ramanspektroskopi
- Röntgenemissionspektroskopi



