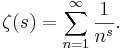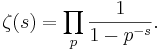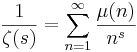Riemanns zeta-funktion

Från Rilpedia

(Omdirigerad från Riemann zeta funktion)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Riemanns zeta-funktion ζ(s) definieras för alla komplexa tal s med realdel större än 1 som

\zeta(s) = \sum_{n=1}^\infin \frac{1}{n^s}.

Riemann upptäckte att denna serie har en analytisk fortsättning för alla s skilda från 1. Denna fortsättning är vad som ligger till grund för Riemannhypotesen.

Euler upptäckte att serien ovan även kan uttryckas som en oändlig produkt över alla primtal,

\zeta(s) = \prod_{p} \frac{1}{1-p^{-s}}.

Man kan uttrycka det inverterade värdet av zeta-funktionen med hjälp av Möbiusfunktionen μ(n) på följande sätt:

\frac{1}{\zeta(s)} = \sum_{n=1}^{\infin} \frac{\mu(n)}{n^s}

för varje komplext tal s med realdel > 1.

E-to-the-i-pi.svg Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Riemanns_zeta-funktion"
Personliga verktyg