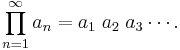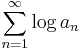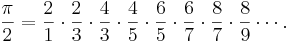Oändlig produkt

Från Rilpedia

Texten från svenska Wikipedia

En oändlig produkt är inom matematiken en produkt som innehåller ett oändligt antal faktorer. Om a_n betecknar den nte faktorn, kan en sådan produkt kan skrivas

$\prod_{n=1}^{\infty} a_n = a_1 \; a_2 \; a_3 \cdots.$

Den oändliga produkten definieras som gränsvärdet av delprodukterna a₁a₂...a_n då n går mot oändligheten. Produkten konvergerar om logaritmen

$\sum_{n=1}^{\infty} \log a_n$

gör det. Undantagsfallet är då någon faktor är 0, i vilket fall produkten är 0.

Exempel på välkända oändliga produkter är Viètes formel för talet π,

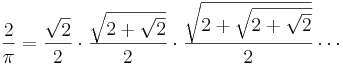$\frac{2}{\pi} = \frac{ \sqrt{2} }{ 2 } \cdot \frac{ \sqrt{2 + \sqrt{2}} }{ 2 } \cdot \frac{ \sqrt{2 + \sqrt{2 + \sqrt{2}}} }{ 2 } \cdots$ ,

och Wallis formel för detsamma,

$\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots.$

Oändlig produkt

Från Rilpedia

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk