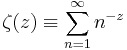Riemannhypotesen
Från Rilpedia
Riemannhypotesen är en matematisk hypotes som även kallas Riemanns zeta-hypotes. Den formulerades först av Bernhard Riemann år 1859.
Hypotesen behandlar indirekt primtalens förekomst ibland de naturliga talen (de positiva heltalen). Rent konkret handlar det dock om att hitta alla nollställen till Riemanns zeta-funktion. Zetafunktionen definieras för komplexa tal z med Re z>1 genom summan
och kan sedan fortsättas analytiskt till en funktion som är analytisk överallt utom för z=1, där den har en enkel pol.
"Triviala" lösningar är de negativa, jämna heltalen (-2, -4, -6 ...). Alla andra till dags dato kända lösningar har realdelen 1/2, och hypotesen påstår att samtliga lösningar antingen är de ovan nämnda reella, negativa talen, eller är ett komplext tal med realdelen 1/2 (dessa lösningar kallas hädanefter för de icketriviala lösningarna). Man vet hittills bland annat att de icketriviala lösningarna måste uppfylla 0 ≤ Re(z) < 1.
Det är fortfarande inte känt huruvida hypotesen är sann eller inte, och problemet räknas till de absolut största inom matematiken idag. Clay Mathematics Institute har utfäst en belöning på en miljon dollar till den som kan strikt visa att hypotesen är antingen korrekt eller felaktig; som ett av de så kallade Millennieproblemen. Problemet fanns även som nummer 8 på David Hilberts lista över 23 olösta problem från år 1900.