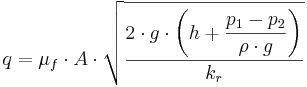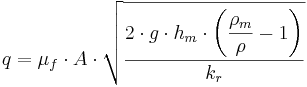Rörknä
Från Rilpedia
Rörknä är en mycket enkel flödesbestämningsmetod där man utnyttjar den tilläggsförlust som alltid sker i en rörkrökspassage. Då det inte sker någon förändring av diametern, förblir hastigheten konstant genom rörknät enligt kontinuitetsekvationen. Genom att mäta upp det statiska trycket strax före och strax efter rörknät med piezometeröppningar, kan flödet beräknas genom följande ekvation:
där
q = Flöde (m3)
цf = Koefficient för rörknäts tilläggsförluster (-)
A = Inre tvärsnittsarea vid rörknät (m2)
g = Tyngdacceleration (m/s2)
h = Höjdskillnad mellan rörets centrum vid mätpunkt 1 och mätpunkt 2 (mVp)
p1 = Statiskt tryck strax före rörknät (Pa)
p2 = Statiskt tryck strax efter rörknät (Pa)
k/r = Förlustterm för rörkrökspassage (-)
I denna form blir flödet beroende av hur rörknät lutar. Om man istället avläser den statiska tryckskillnaden med en piezometerring på både före och rörknät samt använder en manometervätska för avläsningen, kan effekterna på rörknäts lutning "trollas bort". Då ser flödesekvationen ut enligt följande:
där
q = Flöde (m3)
цf = Koefficient för rörknäts tilläggsförluster (-)
A = Inre tvärsnittsarea vid rörknät (m2)
g = Tyngdacceleration (m/s2)
hm = Avläst höjdskillnad mellan mätpunkt 1 och mätpunkt 2 (meter vätskepelare)
ρm = Manometervätskans densitet (kg/m3)
k/r = Förlustterm för rörkrökspassage (-)
För att erhålla rätt avläsning, bör rörledningen vara rak i åtminstone 30 diametrars längd uppströms rörknät. Dessutom bör rörknät kallibreras på mätplatsen. När rörknät väl är kalibrerat, blir mätnoggrannheten lika hög som ett venturirör.