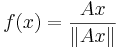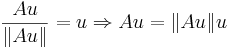Perron-Frobenius sats
Från Rilpedia
Inom matematiken är Perron-Frobenius sats en sats om icke-negativa och positiva matriser, uppkallad efter matematikerna Oskar Perron och Ferdinand Georg Frobenius.
För positiva matriser
Låt A vara en positiv kvadratisk matris. Då gäller:
- Det finns ett positivt egenvärde λ till A som har en tillhörande positiv egenvektor v.
- λ är till beloppet större än alla andra egenvärden till A.
- Alla andra positiva egenvektorer till A är en multipel av v.
- λ har algebraisk multiplicitet 1.
För icke-negativa matriser
Låt A vara en icke-negativ kvadratisk matris. Då gäller:
- Det finns ett positivt egenvärde λ till A som har en tillhörande icke-negativ egenvektor v.
- λ är till beloppet större än eller lika med alla andra egenvärden till A.
- Alla andra positiva egenvektorer till A är en multipel av v.
- λ har algebraisk multiplicitet 1.
Om A är en irreducibel matris så gäller att v inte bara är icke-negativ, utan positiv.
Bevisskiss
Bevisskiss att satsen gäller i 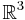 .
.
Givet är en icke-negativ 3x3-matris A. Vi tar en icke-negativ vektor v. Det inses lätt att avbildningen Av då också är icke-negativ, dvs avbildar den första oktanten på sig själv. Vi definierar funktionen:
Värdemängden till f(x) är då enbart enhetsvektorer, och vi ser att f(x) avbildar mängden av alla enhetsvektorer i första oktanten på sig själv, dvs mängden 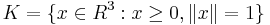 , med andra ord den del av enhetssfären som ligger i första oktanten. Denna mängd är homeomorf med en skiva i planet. Vi kan då använda Brouwers fixpunktssats, som säger att det finns ett u så att f(u) = u, vilket ger att:
, med andra ord den del av enhetssfären som ligger i första oktanten. Denna mängd är homeomorf med en skiva i planet. Vi kan då använda Brouwers fixpunktssats, som säger att det finns ett u så att f(u) = u, vilket ger att:
Dvs, u som ligger i första oktanten (och därför är icke-negativ) är en egenvektor, och har egenvärdet 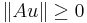 (eftersom
(eftersom 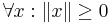 ). Alltså har A en positiv egenvektor med tillhörande positivt egenvärde.
). Alltså har A en positiv egenvektor med tillhörande positivt egenvärde.