Peanos kurva
Från Rilpedia
Peanos kurva upptäcktes 1890 av den italienske matematikern Giuseppe Peano och det var den första kontinuerliga kurvan som kunde täcka en hel kvadrat. Peanos upptäckt har sedan gett upphov till flera andra rumsfyllande kurvor både i planet och i högre dimensioner. Rumsfyllande kurvor av dimension 2 kallas dock ofta för Peanos kurvor till upptäckarens ära.
Innehåll |
Bakgrund
1878 gjorde den rysk-tyske matematikern Georg Cantor en intressant upptäckt. Han fann att två ändliga, släta mångfalder oberoende av dess dimensioner har samma kardinalitet. Vilket med enklare språk betyder att två ytor av ändlig dimension t.ex. en linje och ett plan innehåller lika många punkter. Detta innebär att man skulle kunna avbilda enhetslinjen [0,1] på enhetskvadraten [0,1]2 bijektivt. Det vill säga att varje element i [0,1] motsvarar ett och endast ett element i [0,1]2 och tvärtom.
Cantors upptäckt skapade en mängd frågor, t.ex. kan en sådan avbildning vara kontinuerlig? Eugen Netto visade 1879 inga sådana kontinuerlig kurvor existerade om bijektiviteten skulle uppfyllas. Då undrade man om det fanns kontinuerliga avbildningar då bijektiviteten sänktes till surjektivitet. Alltså om det fanns kontinuerliga avbildningar från enhetslinjen till enhetskvadraten som passerar varje punkt i kvadraten. Peano fann 1890 att sådana kurvor existerade.
Grafisk tolkning av Peanos kurva
Peano gjorde sin upptäckt analytiskt, det är dock lättare att förstå kurvans innebörd grafiskt. Den tyske matematiker David Hilbert var den första som insåg hur man kunde skapa kurvorna geometriskt. Han förstod att om enhetslinjen kan avbildas kontinuerligt på enhetskvadraten, kan man dela upp enhetslinjen i fyra lika stora intervall och avbildningen från dessa skulle hamna i fyra lika stora underkvadrater. Dessa kan sen i sin tur delas upp i fyra nya delar. När man delat intervallen och kvadraterna så de blivit godtyckligt små har man fått en peano kurva. Bilden visar hur man genererar en sådan kurva enligt Hilberts idé. Fast till skillnad från Hilbert använder bilden nio underkvadrater men principen är densamma.
Definition av Peanos kurva
Peanos kurva avbildar ![f:[0,1]\rightarrow [0,1]^2](/w/images/sv.rilpedia.org/math/2/4/8/248240f4fcacb804954ed64e43e3d9d7.png) och funktionen är definierat enligt ett trinärt system,
och funktionen är definierat enligt ett trinärt system,
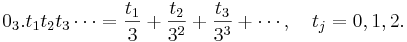
Peano skapade sin avbilning med hjälp av operatorn,
Peanos kurva avbildar ett trinärt bråk på en punkt i enhetskvadraten enligt
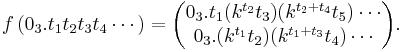
Där kv beteknar den vte iterationen av k.
För att avbildningen ska vara en rumsfyllande kurva måste den vara surjektiv och kontinuerlig. Så för att bevisa att Peanos kurva är en rumsfyllande kurva bevisas först att den är surjektiv och sedan att den är kontinuerlig.
Bevis att Peanos kurva är rumsfyllande
Surjektivitet
Tag en godtycklig punkt i enhetskvadraten,
![(0_3.\beta_1\beta_2\beta_3\beta_4\cdots,0_3.\gamma_1\gamma_2\gamma_3\gamma_4\cdots) \in [0,1]^2.](/w/images/sv.rilpedia.org/math/e/0/5/e05550f67f38b1a66c352c2d8beff9ee.png)
Det ska då finnas åtminestone en punkt på enhetslinjen
![t=0_3.t_1t_2t_3t_4\cdots \in [0,1]](/w/images/sv.rilpedia.org/math/b/b/b/bbb09321f01ce3295a1686acee22e090.png)
sådan att
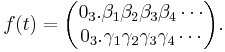
Genom att jämföra f(t) med Peanos definition erhåller man följande rekursiva samband:
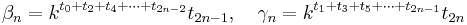 där t0 = 0
där t0 = 0Sambanden kan sen inverteras eftersom
Det vill säga k är sin egen invers vilket ger
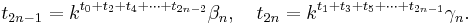
Nu går det att lösa för 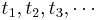 och därav är f surjektiv.
och därav är f surjektiv.
Kontinuitet
Vi skriver Peanos kurva som
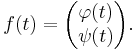
För att kurvan ska vara kontinuerlig måste både 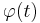 och ψ(t) vara det på hela [0,1]. Funktionen
och ψ(t) vara det på hela [0,1]. Funktionen 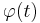 bevisas vara kontinuerlig genom att låta
bevisas vara kontinuerlig genom att låta
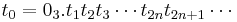 och
och 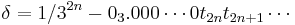
Detta ger
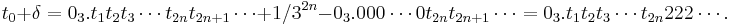
Om vi nu har ![t \in [t_0, t_0+\delta]](/w/images/sv.rilpedia.org/math/2/3/d/23d04ae8864a0c5c80bbc1ec378fd7ff.png) kommer t stämma överens med t0 de första 2n sifftorna och därför kan man uttrycka t som,
kommer t stämma överens med t0 de första 2n sifftorna och därför kan man uttrycka t som,
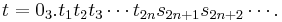
För att se om 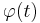 är kontinuerlig sätter vi
är kontinuerlig sätter vi
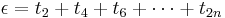
och tittar sedan på 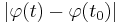 som ska gå mot noll om
som ska gå mot noll om 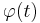 är kontinuerlig.
är kontinuerlig.
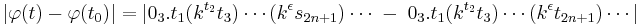
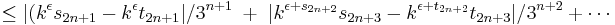
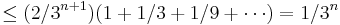
Vilket ger gränsvärdet,
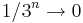 då
då 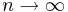
.
Alltså är 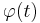 kontinuerlig från höger, för att ta reda på om den är kontinuerlig från vänster gör man på samma sätt, men tar t − δ istället. Gör man det finner man att
kontinuerlig från höger, för att ta reda på om den är kontinuerlig från vänster gör man på samma sätt, men tar t − δ istället. Gör man det finner man att 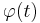 är kontinuerlig på hela [0,1]. Att
är kontinuerlig på hela [0,1]. Att 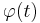 är kontinuerlig medför att ψ(t) är det också eftersom
är kontinuerlig medför att ψ(t) är det också eftersom 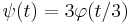 . Därmed är hela beviset klart.
. Därmed är hela beviset klart.
Fraktaler
Peanos kurva var en av de första fraktalerna och lade grunden för fraktalteorin som långt efter Peanos upptäckt fått otaliga tillämpningar. Fraktaler används idag inom många vetenskapliga områden t.ex. datorvetenskap och medicin.
Referenser
Sagan, Hans (1994), Space-Filling Curves, Springer-Verlag, Mall:MR, ISBN 0387942653.




