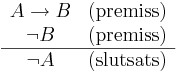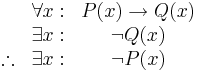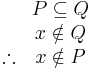Modus tollens

Satslogiska härledningsregler
	Modus ponens; Modus tollens; Och-eliminering; Och-introducering; Eller-eliminering; Eller-introducering; Dilemma;

Texten från svenska Wikipedia

Modus tollens (latin: metod för förnekande) är en logisk härledningsregel med formen:

$\begin{array}{cc} A \rightarrow B & \mathrm{(premiss)}\\ \neg B & \mathrm{(premiss)}\\ \hline \neg A & \mathrm{(slutsats)}\\ \end{array}$

Första raden utläses "Om A så B" eller "A implicerar B". Pilen står för implikation. Andra raden utläses "icke B" och tredje raden "icke A".

Regeln är starkt relaterad till egenskapen kontraposition hos den klassiska materiella implikationen att A → B är ekvivalent med ¬B → ¬A.

Inom predikatlogik finns följande formulering:

$\begin{array}{ccc} & \forall x: & P(x) \rightarrow Q(x) \\ & \exists x: & \neg Q(x) \\ \therefore & \exists x: & \neg P(x) \end{array}$

Vilket kan utläsas: Allt som uppfyller P uppfyller Q. Det finns ett x som inte uppfyller Q. Alltså finns ett x som inte uppfyller P.

I mängdlära kan det uttryckas som:

$\begin{array}{cc} & P \subseteq Q \\ & x \notin Q \\ \therefore & x \notin P \end{array}$

dvs, P är en delmängd till Q. x är inte ett element i Q. Alltså är x inte ett element i P.