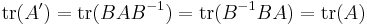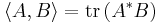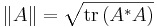Spår (matematik)

Från Rilpedia

(Omdirigerad från Matrisspår)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Spåret är inom matematiken summan av diagonalelementen i en kvadratisk matris. Dvs, givet matrisen $A$ av storlek $n$ med elementen $a i j$ , så är spåret:

$\operatorname{tr} \, A = \sum_{k = 1}^n a_{kk}$

Beteckningen 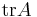$\operatorname{tr} A$ kommer från engelskans trace. Även beteckningen 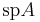$\operatorname{sp} A$ efter tyskans spur förekommer.

Egenskaper

För spåret av $A$ gäller:

$\operatorname{tr} \, (A)=\operatorname{tr} \,(A^T)$ .
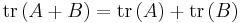$\operatorname{tr} \,(A+B)=\operatorname{tr} \,(A)+\operatorname{tr} \,(B)$ .
$\operatorname{tr} \,(\alpha A)=\alpha \operatorname{tr} \,(A)$ .
$\operatorname{tr} \,(ABC) =\operatorname{tr} \,(CAB) = \operatorname{tr} \,(BCA)$ .

Observera att den sista egenskapen inte är kommutativitet, matriserna får inte byta plats hur som helst, man får dock flytta dem cykliskt (matrisen som står först får sättas sist och vice versa).

Man kan visa att spåret är invariant under similärtransformation, dvs en transformation av formen:

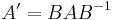$A'= BAB^{-1}\,$ .

Eftersom:

$\operatorname{tr}(A') = \operatorname{tr}(BAB^{-1}) = \operatorname{tr}(B^{-1}BA) = \operatorname{tr}(A)$

Härav följer att spåret av $A$ är lika med summan av egenvärdena till $A$ , $\lambda_1, \dots \lambda_n$ :

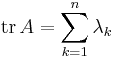$\operatorname{tr} \, A = \sum_{k=1}^n \lambda_k$ .

Detta inses lätt för diagonaliserbara matriser. All matriser kan dock skrivas på Jordans normalform (alternativt kan man använda Schurs sats), då matrisen genom en similärtransformation omvandlas till en matris på en blockdiagonal form med egenvärdena i diagonalen, så att formeln ovan följer.

Användning

Med spåret av en matris kan man definiera en inre produkt i vektorrummet av alla komplexa (eller reella) matriser av format 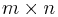$m \times n$ genom:

$\langle A,B \rangle = \operatorname{tr} \, (A^* B)$

Där $A *$ är det hermiteska konjugatet av $A$ . Genom den inre produkten kan man inducera en matrisnorm:

$\|A\| = \sqrt{\operatorname{tr} \, (A^* A)}$

som är samma norm som Frobeniusnormen.

Generalisering

Spårkonceptet kan generaliseras till spårklassen av kompakta operatorer i Hilbertrum.

Spår (matematik)

Från Rilpedia

Egenskaper

Användning

Generalisering

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk