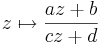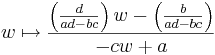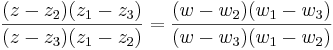Möbiusavbildning

Från Rilpedia

(Omdirigerad från Möbiustransformation)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

En Möbiusavbildning eller Möbiustransformation, efter August Ferdinand Möbius, är en bijektiv konform avbildning av det utökade komplexa talplanet (komplexa talen utökade med en punkt i oändligheten) på sig självt.

En Möbiusavbildning bevarar vinklar och cirklinjer (räta linjer ses som cirklar som passerar oändlighetspunkten).

En Möbiusavbildning är en rationell funktion

$z\mapsto \frac{az+b}{cz+d}$

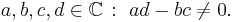där $a,b,c,d \in \mathbb{C} \,:\ ad-bc \neq 0.$ Följande gäller generellt för denna avbildning

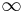
punkten $z = - d / c$ avbildas på $\infty$
punkten 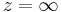$z=\infty$ avbildas på $a / c$

Villkoret 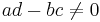$ad-bc \neq 0$ är nödvändigt för att transformationen skall vara inverterbar. Den inversa avbildningen ges av

$w \mapsto \frac{\left(\frac{d}{ad-bc}\right) w - \left(\frac{b}{ad-bc}\right)}{-c w + a}$

En Möbiusavbildning bestäms entydigt om man anger tre punkter och vilka punkter de avbildas på, enligt följande: Låt $z 1$ , $z 2$ och $z 3$ vara de tre ursprungliga punkterna och $w 1$ , $w 2$ respektive $w 3$ vara de punkter de skall avbildas på. Då kan avbildningen skrivas

$\frac{(z-z_2)(z_1-z_3)}{(z-z_3)(z_1-z_2)} = \frac{(w-w_2)(w_1-w_3)}{(w-w_3)(w_1-w_2)}$

Spegelpunkter

Definiera här spegelpunkten till ett komplext tal $z$ relativt en cirkel med radie $r$ och centrum $z 0$ som det tal $z *$ som uppfyller följande:

$z 0$ , $z$ , och $z *$ ligger på samma linje.
$| z - z O | | z * - z 0 | = r 2$

Man definierar dessutom 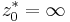$z_0^* = \infty$ . Om speciellt cirkeln är en linje $L$ , så definiera $z *$ som det tal som ligger på normalen till $L$ som går genom $z$ , och som ligger lika långt från $L$ som $z$ , men på andra sidan. Exempelvis gäller 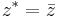$z^* = \bar{z}$ om $l$ är reella tallinjen. 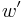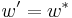Möbiusavbildningar överför $z$ och dess spegelpunkt $z *$ relativt en cirkel $C$ på punkter $w$ och $w^\prime$ , där $w^\prime = w^*$ relativt bilden av $C$ (som är en cirkel).