Linjärkombination

Från Rilpedia

(Omdirigerad från Linjärt hölje)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

I matematik är linjärkombination ett centralt begrepp inom linjär algebra och närliggande områden. Det definieras som följer:

Låt V1 , V2 , ... , Vn vara givna vektorer.

En vektor av formen c1V1 + c2V2 + ... + cnVn, där c1 , c2 , ... cn är godtyckliga skalärer, kallas en linjärkombination av vektorerna V1 , V2 , ... , Vn.

Innehåll

Exempel

Vektorer

En vektor kan delas upp i komponenter med hjälp av en linjärkombination. Till exempel

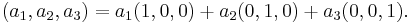
\,(a_1,a_2,a_3)=a_1(1,0,0)+a_2(0,1,0)+a_3(0,0,1).

Funktioner

Funktioner kan skrivas om i andra funktioner med hjälp av linjärkombination, några enkla exempel är

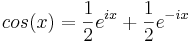
  • cos(x)=\frac{1}{2}e^{ix}+\frac{1}{2}e^{-ix}
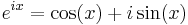  • \;e^{ix}=\cos (x)+i\sin (x).

Polynom

Om man väljer 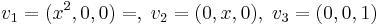\;v_1=(x^2,0,0)=,\; v_2=(0,x,0),\; v_3=(0,0,1) så kan man skriva

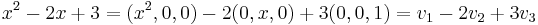
\;x^2-2x+3=(x^2,0,0)-2(0,x,0)+3(0,0,1)=v_1-2v_2+3v_3

Linjärt hölje

Mängden av alla linjärkombinationer kallas linjärt hölje. Låt 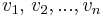v_1,\, v_2,..., v_n vara i vektorer i något vektorrum V och 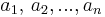a_1,\, a_2,..., a_n skalärer i någon skalärkropp, K. Då är det linjära höljet

\; [v_1, v_2,..., v_n]=\{ a_1v_1+a_2v_2+... + a_nv_n:a_1,a_2,...,a_n\epsilon K\}.

Se även


Nuvola apps edu mathematics-p.svg Denna artikel om algebra är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Linj%C3%A4rkombination"
Personliga verktyg