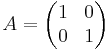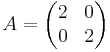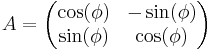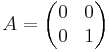Linjär avbildning
Från Rilpedia
Inom matematiken är en linjär avbildning (även kallad linjär transformation och linjär operation) en särskild sorts avbildning mellan två vektorrum.
Innehåll |
Definition
En linjär avbildning F är en avbildning som uppfyller följande för vektorer x,y och skalärer α,β:
- F(αx) = αF(x)
- F(x + y) = F(x) + F(y)
Dessa två krav skrivs ibland ihop till ett krav:
- F(αx + βy) = αF(x) + βF(y)
En direkt följd av definitionen är att F(0) = 0 om F är en linjär avbildning.
Exempel
Exempel på linjära avbildningar är:
- För reella tal är
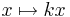 för en konstant k en linjär avbildning.
för en konstant k en linjär avbildning. - En matris med storlek
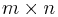 definierar en avbildning från ett n-dimensionellt vektorrum till ett m-dimensionellt vektorrum.
definierar en avbildning från ett n-dimensionellt vektorrum till ett m-dimensionellt vektorrum. - Derivering och Integration.
- Laplace- och Fouriertransformation.
Exempel på avbildningar som inte är linjära är:
- För reella tal:
 och
och 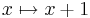 . Ibland missuppfattas den senare avbildningen som "linjär", därför att dess funktionsgraf är en linje. Denna egenskap gör dock bara funktionen till en affin avbildning.)
. Ibland missuppfattas den senare avbildningen som "linjär", därför att dess funktionsgraf är en linje. Denna egenskap gör dock bara funktionen till en affin avbildning.)
Avbildningsmatriser
Som nämnts ovan kan matriser representera avbildningar. Här är några exempel på avbildningar 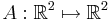 :
:
- Identitesavbildning (avbildar en vektor på samma vektor):
- Skalning två gånger i alla riktningar:
- Rotation med vinkeln φ moturs:
- Projektion på y-axeln:
Tillämpningar
Linjära transformationer användas bland annat för att skapa linjära fraktaler som till exempel von Kochs kurva. För att genomföra detta så brukas ett itererat funktionssystem (IFS) som består av två eller flera linjära transformationer av samma eller olika typ.