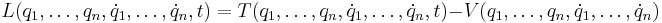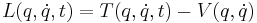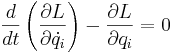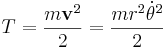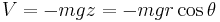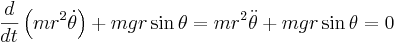Lagrangefunktion
Från Rilpedia
Lagrangefunktionen är en funktion som används för att formulera om den klassika mekaniken. Den kan vara ett väldigt kraftfullt sätt att ta fram rörelseekvationerna för ett system, och används för att ta fram Hamiltonfunktionen, som är lämplig för att vinna insikt i den klassiska mekaniken. Eftersom den använder generaliserade variabler så är den ofta lämplig att använda på system där kartesiska koordinater inte är det mest naturliga valet.
Lagrangefunktionen skrivs oftast som den kinetiska energin minus den potentiella energin:
vilket ofta skrivs mer kompakt som
Rörelseekvationerna för systemet fås sedan av Euler-Lagranges ekvationer:
Exempel
För en endimensionell pendel är det naturligt att använda polära koordinater 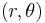 . Skriven i sådana är de kinetiska och potentiella energierna
. Skriven i sådana är de kinetiska och potentiella energierna
(notera att 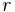 är fix varför endast
är fix varför endast 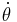 -termen dyker upp i hastigheten).
-termen dyker upp i hastigheten).
Detta ger lagrangefunktionen
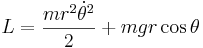 .
.
Stoppar man in detta i Euler-Lagranges ekvation får man
vilket är den helt korrekta ekvationen för pendelns rörelse.