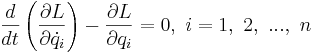Euler-Lagranges ekvationer

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Euler-Lagranges ekvationer, eller bara Lagranges ekvationer, är en omformulering av Newtons rörelseekvationer, som via förarbete av Leonhard Euler fick sin slutgiltiga formulering 1788 av Joseph Louis Lagrange.

För ett system med n frihetsgrader beskrivet av n generaliserade koordinater qi uttrycks Lagrangefunktionen L, i de generaliserade koordinaterna qi och dess derivator med avseende på tiden 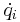\dot{q}_i, som skillnaden mellan den kinetiska och den potentiella energin. När summan av alla yttre krafter som verkar på systemet är noll har Lagranges ekvationer formen

\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i} \right)-\frac{\partial L}{\partial q_i}=0, ~ i = 1, ~ 2, ~..., ~n


Gnome-system-run.svg Denna mekanikartikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Euler-Lagranges_ekvationer"
Personliga verktyg