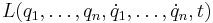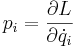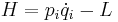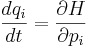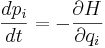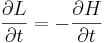Hamiltonfunktion

Från Rilpedia

Texten från svenska Wikipedia

Hamiltonfunktionen är en funktion, uppkallad efter William Rowan Hamilton som beskriver klassisk mekanik på ett sätt som gör den bättre lämpad än Lagrangefunktionen för att utvidga den mekaniska teorin, men å andra sidan sämre att använda på specifika problem. Den kan, men behöver inte, motsvara den totala energin för ett system, vanligen uppdelad i potentiell och kinetisk energi.

I kvantmekaniken motsvaras den av Hamiltonoperatorn.

Rörelseekvationer

Rörelseekvationerna för Hamiltonsk mekanik härleds ur de för Lagrangsk mekanik - Euler-Lagranges ekvationer. Idén är att man börjar med en Lagrangefunktion beroende av generaliserade lägesvariabler 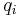$q_i \$ , dessas tidsderivator 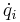$\dot{q}_i\,$ , samt tiden $t\,$ :

$L(q_1,\dots ,q_n,\dot{q}_1,\dots,\dot{q}_n,t)\,$

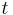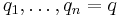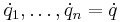Det är vanligt att man sätter $q_1,\dots ,q_n=q\,$ och $\dot{q}_1,\dots,\dot{q}_n=\dot{q}$ för att förkorta uttrycken

Sedan definierar man generaliserad rörelsemängd 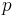$p\,$ som

$p_i=\frac{\partial L}{\partial \dot{q}_i}$

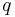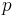Via en legendretransform kan man nu komma fram till ett uttryck för en funktion som bara beror på de numera oberoende variablerna $q\,$ och $p\,$ , men inte på 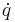$\dot{q}$ . Denna funktion är en hamiltonfunktion för systemet: