Lådräkningsdimension

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Lådräkningsdimension (eng. box-counting dimension), kallas även Minkowski-Bouliganddimension.

Definition

Tag en mängd F i ett rektangulärt område. Lägg ett rutnät på detta område med bredden δ0 på rutorna. Kalla nu antalet rutor som innehåller någon del av F för 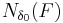N_{\delta_0}(F).

Vad händer då vi gör rutnätet mindre? Hur förändras N(F)? Om F är en linje, som är endimensionell, kommer N(F) att fördubblas om rutnätet görs dubbelt så fint. Är i stället F en tvådimensionell mängd, till exempel en rektangel, kommer N(F) öka med en faktor 22 = 4. För en tredimensionell kub blir ökningen i stället 23 = 8 osv.

Om föregående stycke generaliseras till en godtycklig dimension D och rutnätets upplösning förändras från δ0 till δ erhålls uttrycket

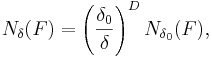
N_{\delta}(F) = \left( \frac{\delta_0}{\delta} \right) ^ D N_{\delta_0}(F),

då 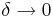\delta \to 0, vilket är samma resultat som precis resonerades fram. Nu tar vi logaritmen av båda leden:

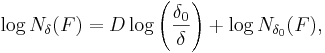
\log N_{\delta}(F) = D\log \left( \frac{\delta_0}{\delta} \right) + \log N_{\delta_0}(F),

som efter omskrivning får formen

\log N_{\delta}(F) = D \cdot (-\log\delta) + \log \left( \delta_0 ^ D \cdot N_{\delta_0}(F)\right).


Sambandet mellan − logδ och logNδ(F) är alltså en rät linje, med riktningskoefficienten D. Detta gör att lådräkningsdimensionen är mycket lätt att beräkna numeriskt utifrån bilder.

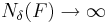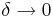Det bör påpekas att eftersom N_\delta(F) \to \infty om \delta \to 0 och D > 0, så kan föregående samband skrivas som

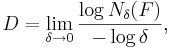
D = \lim_{\delta \to 0} \frac{\log N_\delta(F)}{-\log \delta},

vilket är den definition som brukar hittas i litteratur.

Detta dimensionsbegrepp heter egentligen Minkowski-Bouligand-dimension och hänger starkt samman med Hausdorff-dimensionen. För alla mängder är 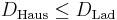D_{\operatorname{Haus}}\leq D_{\operatorname{Lad}} och likhet råder för många fraktaler. Ett exempel där likhet inte råder är den uppräkningsbara mängden 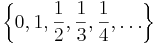\left\{0,1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\ldots\right\}, som har lådräkningsdimension 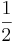\frac{1}{2}, men Hausdorffdimension lika med, kanske lite mer intuitivt, 0.

Tillämpningar

Beräkning av dimension på skånes kust

Detta dimensionsbegrepp kan användas för att numeriskt räkna ut dimensionen på mängder, till exempel fraktaler. Eftersom kvadratiska "lådor" används är denna definition lämplig för datorer, till skillnad från Hausdorffdimensionen, som täcker över med mängder av godtycklig form.

Vill man beräkna en kuststräckas dimension, är det detta dimensionsbegrepp man använder.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/L%C3%A5dr%C3%A4kningsdimension"
Personliga verktyg