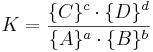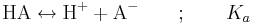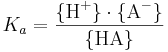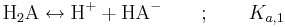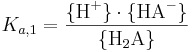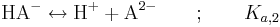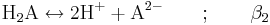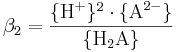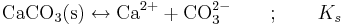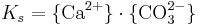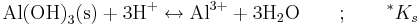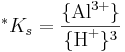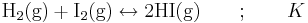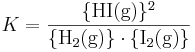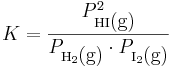Jämviktskonstant

Från Rilpedia

(Omdirigerad från Jämviktsekvation)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Jämviktskonstanten beskriver förhållandet mellan produkter och reaktanter i en kemisk jämviktsreaktion.

Ett exempel på en kemisk jämvikt är:

aA + bB  Dubbelpil  cC + dD

där a, b, c och d är de stökiometriska koefficienterna för respektive ämne, vilka betecknas med A, B, C respektive D och där A och B är reaktanter och C och D är produkter (se även kemisk jämvikt). Jämviktskonstanten definieras på följande sätt, med produkterna i täljaren och reaktanterna i nämnaren:

K = \frac{{\{C\}^c \cdot \{D\}^d }}{{\{A\}^a \cdot \{B\}^b }}

där K är jämviktskonstanten; {A}, {B}, {C} och {D} är aktiviteterna av ämnena A, B, C samt D.

Med denna definition finns ett direkt förhållande mellan Gibbs fria energi och jämviktskonstanten enligt följande:

ΔG = −RT ln K

Värdet på konstanten är endast giltigt vid konstant temperatur och tryck. Det värde för K som ges i tabeller och datasammanställningar är vanligen giltigt för 25 grader och för 1 atm, och olika metoder finns för att korrigera konstanterna till aktuella förhållanden.

Innehåll

Syrakonstant

För en enprotonig syra, det vill säga för en syra HA som dissocierar i endast ett steg, kan vi skriva följande generella jämviktsreaktion:

\mbox{HA} \leftrightarrow \mbox{H}^+ + \mbox{A}^- \qquad ; \qquad K_{a}

Jämviktskonstanten Ka benämns även syrakonstant. Av den allmänna definitionen av jämviktskonstanten ovan följer att:

K_{a} = \frac{{\{\mbox{H}^+\} \cdot \{\mbox{A}^-\} }}{{\{\mbox{HA}\}}}

Minuslogaritmen av Ka, det vill säga -log10 Ka, är det så kallade pKa-värdet. Detta värde motsvarar det pH-värde då syran dissocierat till 50 %, det vill säga då {HA} = {A-}.

En tvåprotonig syra H2A dissocierar i två steg. Det första steget skrivs:

\mbox{H} _2 \mbox{A} \leftrightarrow \mbox{H}^+ + \mbox{HA}^- \qquad ; \qquad K_{a,1}

där Ka,1 definieras på motsvarande sätt som för en enprotonig syra, nämligen:

K_{a,1} = \frac{{\{\mbox{H}^+\} \cdot \{\mbox{HA}^-\} }}{{\{\mbox{H} _ 2 \mbox{A}\}}}

Det andra steget kan skrivas på två sätt; antingen utgår man från HA-:

\mbox{HA}^- \leftrightarrow \mbox{H}^+ + \mbox{A}^{2-} \qquad ; \qquad K_{a,2}

där Ka,2 definieras som:

K_{a,2} = \frac{{\{\mbox{H}^+\} \cdot \{\mbox{A}^{2-}\} }}{{\{\mbox{HA}^-\}}}

Alternativt kan man utgå från H2A och man får:

\mbox{H} _2 \mbox{A} \leftrightarrow 2\mbox{H}^+ + \mbox{A}^{2-} \qquad ; \qquad \beta_2

Jämviktskonstanten benämns i litteraturen ofta som β så fort två eller fler vätejoner är inblandade i reaktionen. Konstanten β2 definieras som:

\beta_2 = \frac{{\{\mbox{H}^+\}^2 \cdot \{\mbox{A}^{2-}\} }}{{\{\mbox{H} _2 \mbox{A}\}}}

Syrakonstanterna för tre- och fyraprotoniga syror definieras på motsvarande sätt.

Löslighetskonstant

Definition

Löslighetskonstanten är en form av jämviktskonstant som talar om hur löslig en utfällning är vid jämvikt. Som exempel kan tas kalcit, CaCO3(s), vars löslighet regleras av följande jämvikt:

\mbox{CaCO} _3 \mbox{(s)} \leftrightarrow \mbox{Ca}^{2+} + \mbox{CO}_3^{2-} \qquad ; \qquad K_s

Vid definitionen av löslighetskonstanten Ks ska man komma ihåg att aktiviteten för en fast fas = 1 då utfällningen är ideal (vilket vanligen antas). Detta betyder att aktiviteten för CaCO3(s) försvinner ur nämnaren och vi får:

K_s = \{ \mbox{Ca}^{2+} \} \cdot \{ \mbox{CO}_3^{2-} \}

En löslighetskonstant som uttrycks på detta sätt (som en produkt) kallas också för en löslighetsprodukt. För kalcit är värdet på Ks = 10-8,48 vid 25 grader och trycket 1 atm.

Ibland, särskilt för oxider och sulfider, skrivs löslighetskonstanter med vätejoner i vänsterledet i stället för med hydroxidjoner i högerledet. Konstanterna benämns då *Ks. Poängen med detta skrivsätt är att vätejonerna i princip är mätbara genom pH. Som exempel kan tas löslighetskonstanten för gibbsit, Al(OH)3(s):

\mbox{Al(OH)} _ 3 \mbox{(s)} + 3 \mbox{H}^+ \leftrightarrow \mbox{Al}^{3+} + 3 \mbox{H}_2 \mbox{O} \qquad ; \qquad ^* K_s

som definieras på följande sätt:

^* K_s = \frac{{\{\mbox{Al}^{3+}\} }}{{\{\mbox{H}^+\}^3}}

Observera att aktiviteten för H2O nästan alltid sätts till 1 enligt konvention, varför den försvunnit ur täljaren. För gibbsit är värdet på *Ks = 10-7.74 vid 25 grader och 1 atm.

Exempel på löslighetskonstanter för utfällningar i vatten

Löslighetskonstanter vid 25 °C (298,15 K) och 1 atm
Namn Formel log10 Ks log10 *Ks
Baryt BaSO4(s) -9,98[1]
Cerrusit PbCO3(s) -13,2[1]
Gibbsit Al(OH)3(s) 7,74[2]
Gips CaSO4×2H2O(s) -4,61[1]
Kalcit CaCO3(s) -8,48[3]
Kalciumhydroxid Ca(OH)2(s) 22,7[1]
Kalciumoxid CaO(s) 32,8[4]
Malakit Cu2(OH)2CO3(s) -5,47[5]
Siderit FeCO3(s) -10,59[5]
Tenorit CuO(s) 7,64[6]

Jämviktskonstant baserad på koncentration

Aktiviteten för ett ämne är relaterad till koncentrationen genom en aktivitetskoefficient, som är beroende av jonstyrkan. Inom lösningskemin är det vanligt att man använder en "jämviktskonstant" som är baserad enbart på koncentrationer – detta för att få en direkt relation mellan mätbara storheter. Detta är möjligt om man har en konstant jonstyrka, eftersom aktivitetskoefficienten är en funktion av jonstyrkan. Denna typ av jämviktskonstant kan skrivas:

K_{(I)} = \frac{{[C]^c \cdot [D]^d }}{{[A]^a \cdot [B]^b }}

där [A], [B], [C] och [D] nu representerar koncentrationer av ämnena i enheten mol/l. Dock är konstanten K(I) starkt beroende av jonstyrkan, och så fort jonstyrkan varierar behövs kunskap om aktivitetskoefficienten.

Jämviktskonstanten för gaser

Aktiviteten för en gas är lika med dess fugacitet. Vid låga tryck och höga temperaturer, förhållanden där Henrys lag är giltig, är fugaciteten lika med partialtrycket, som vanligen anges i bar. Som exempel kan tas bildningen av gasformig vätejodid från vätgas och jod (se kemisk jämvikt):

\mbox{H}_2 \mbox{(g)} + \mbox{I}_2 \mbox{(g)} \leftrightarrow 2 \mbox{HI} \mbox{(g)} \qquad ; \qquad K

Denna konstant definieras enligt:

K = \frac{{\{{\rm{HI} \mbox{(g)}}\}^2}}{{\{{\rm{H_2} \mbox{(g)}}\} \cdot \{{\rm{I_2} \mbox{(g)}}\} }}

där aktiviteterna för gaserna ges av dessas fugaciteter. Vid tillräckligt låga totala tryck, till exempel i jordens atmosfär, är dock fugaciteten lika med partialtrycket för gaserna, och vi får:

K = \frac{{P_{\rm{HI} \mbox{(g)}}^2}}{{P_{\rm{H_2} \mbox{(g)}} \cdot P_{\rm{I_2} \mbox{(g)}} }}

där P står för partialtryck.

Jämviktskonstantens beroende av temperaturen

Jämviktskonstantens temperaturberoende beror mestadels på att Gibbs fria energi för reaktionen är temperaturberoende. Reaktionens entalpiförändring, vilken också inverkar på jämviktskonstanten, varierar betydligt mindre. Vid måttliga avvikelser från standardtillståndet, ungefär i intervallet 0 till 40 grader Celsius, kan van't Hoffs ekvation användas för att uppskatta jämviktskonstantens temperaturberoende:

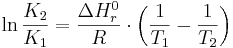
\ln{\frac{K_2}{K_1}} = \frac{\Delta H_r ^0}{R} \cdot \left ( \frac{1}{T_1} - \frac{1}{T_2} \right )

där K1 och K2 är jämviktskonstanterna vid temperaturerna T1 och T2 som anges i Kelvin. ΔHr0 är reaktionens entalpiförändring vid 25 grader (anges i J/mol), och R är den allmänna gaskonstanten med värdet 8,314 J mol-1K-1. Värden för ΔHr0 för olika föreningar återfinns i många databaser och datorprogram för jämviktsberäkningar.

Se även

Källor

Noter

  1. ↑ 1,0 1,1 1,2 1,3 1,4 NIST Critical Stability Constants database 46:8
  2. ↑ Palmer, D.A. and Wesolowski, D.J. 1992. Aluminium speciation and equilibria in aqueous solution: II. The solubility of gibbsite in acidic sodium chloride solutions from 30 to 70°C. Geochim. Cosmochim. Acta 56, 1093-1111.
  3. ↑ Plummer, L.N. and Busenberg, E. 1982. The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90°C, and an evaluation of the aqueous model for the system CaCO3-CO2-H2O. Geochim. Cosmochim. Acta 46, 1011-1040.
  4. ↑ Benjamin, M.M. 2002. Water Chemistry. McGraw-Hill.
  5. ↑ 5,0 5,1 Preis, W. and Gamsjäger, H. 2001. Thermodynamic investigation of phase equilibria in metal carbonate-water-carbon dioxide systems. Monatshefte für Chemie 132, 1327-1346.
  6. ↑ Plyasunova, N.V., Wang, M., Zhang, Y. and Muhammed, M. 1997. Critical evaluation of thermodynamics of complex formation of metal ions in aqueous solutions. II. Hydrolysis and hydroxo-complexes of Cu2+ at 298.15 K. Hydrometallurgy 45, 37-51.

Litteratur

  • M.M. Benjamin. 2002. Water Chemistry. McGraw-Hill.
Hämtad från "https://sv.rilpedia.org/wiki/J%C3%A4mviktskonstant"
Personliga verktyg