Informationsteori
Från Rilpedia
| Det har föreslagits att denna artikel bör slås ihop med Information (mått). (Diskutera) |
Den s.k. statistiska informationsteorin grundlades i mitten av 1900-talet av Claude Shannon som en del av en kommunikationsteori han utvecklade.
Innehåll |
Det diskreta fallet
Det mest kända konceptet är den s. k. entropin inom informationsteorin:
Denna entropi kan beräknas för vilken som helst diskret fördelningsfunktion sådan att summan av alla pi = 1. H blir maximal och lika med logaritmen för antalet pi när alla pi är lika stora. Inom fysiken tolkas entropi också som oordning.
H kan också tolkas som ett medelvärde av information ugående från axiomet att när en händelse inträffar med sannolikheten pi så fås information = -log(pi ). Denna information saknar mental mening och handlar enbart om sannolikheter.
Shannon härledde formeln utifrån axiom som på ett naturligt sätt kan tolkas som information. När vi singlar slant så kan vi få två olika meddelanden vardera med sannolikheten 0.5 och som kan betecknas '0' respektive '1'. Åslund kallar detta ett schema med två lika sannolika händelser. När vi singlar slanten två gånger får vi dubbelt så långa meddelanden - '00', '01', '10' och '11' (ett schema med 4 lika sannolika händelser) - vardera med sannolikheten 0.25.
Ett rimligt antagande (postulat) är att den information som fås i det senare fallet med två tecken per meddelande är lika med summan av informationer som fås från de kortare meddelandena med ett tecken i varje. Ett sätt att få det hela att stämma är att låta information vara den negativa logaritmen av en sannolikhet, ty
-log(0.5) - log(0.5) = -log(0.25); eller log(2) + log(2) = log(4).
Ett annat rimligt antagande är att när meddelandet blir längre så, fås mer information, t. ex. ett singlat meddelande med längden tre fås med sannolikteten 0.125 och ett med längden fyra med sannolikheten 0.0625. Och
-log(0.0625) är större än -log(0.125).
Om en händelse inträffar med sannolikheten 1 (en säker händelse) fås ingen information, ty
-log(1) = 0.
Om detta skall stämma för alla möjliga uppdelningar av meddelanden skrivna med olika alfabeten så blir den negativa logaritmen av en sannolikhet en mycket bra kandidat för att vara ett mått på information.
I det mer generella fallet när sannolikheter i ett schema Y beror av händelser i ett annat schema X, så gäller följande samband för H(Y | X)
H(Y | X) = H(XY) − H(X)
där H(Y | X) är medelvärdet av entropin i Y när X redan har inträffat. Åslund har visat att de enda funktioner som uppfyller samtliga postulat för information är de som är proportionella mot entropin.
Uttrycket för entropi kan då ses som ett medelvärde av information för vilket som helst schema.
Det kontinuerliga fallet
vid övergången från ett diskret schema till en kontinuerlig frekvensfunktion, f(x), kan informationsentropin skrivas
Ett problem här är att log(dx) gör H obestämd och beroende av det oändligt lilla dx. Ett sätt att kringgå problemet är att definiera H så att H blir lika med logaritmen för volymen av ett godtyckligt område, som täcks av en likformig frekvensfunktion, f(x), över området. Detta är i analogi med logaritmen av antalet möjliga lika sannolika händelser i ett diskret schema. Då gäller
Den volym som täcks av en normal frekvensfunktion med momentmatris M är proportionell mot koncentrationsellipsoidens volym och lika med kvadratrot{ (2pie)n determinant(M) }.
Tillämpningar
Exempel på områden där teorin har fått stor betydelse är telekommunikation, datateknik, rymdteknik och biologi. I de flesta fall handlar det om att sända ett meddelande från en sändare till en mottagare, helst felfritt.
Tekniska tillämpningar
Se även
Referenser
- Brooks, D. R. & Wiley, E. O. Evolution as Entropy, Towards a unified theory of Biology. The University of Chicago Press, 1986.
- Shannon, C.E. A Mathematical Theory of Communication, Bell Syst. Techn. J., Vol. 27, pp 379-423, (Part I), 1948.
- Åslund, N. The fundamental theorems of information theory (Swedish). Nordisk Matematisk Tidskrift, Band 9, Oslo 1961.




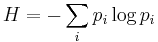
![H = - \int f(x) log[ f(x) dx]dx\](/w/images/sv.rilpedia.org/math/e/9/7/e9786f349168794873f73aee9cd18a40.png)
![H = - \int f(x) log[ f(x)]dx\](/w/images/sv.rilpedia.org/math/f/f/2/ff2c003cfb7ae4d1d85a14d761f3bb49.png)