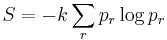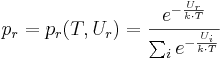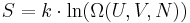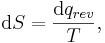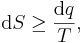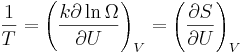Från Rilpedia

Den här artikeln behandlar entropi inom fysiken. För entropi inom informationsteori, se Entropi (informationsteori).För entropi inom organisationsteori, se Entropi (organisationsteori).

Entropi är ett begrepp med ursprung i termodynamiken och kan sägas vara ett mått på oordningen hos ett tillstånd.^[1] Det kan illustreras med ett stökigt rum: I ett fullständigt städat/ordnat rum kan varje sak bara finnas på en plats, det vill säga det finns bara ett sätt att ställa alla saker i rummet så att det har egenskapen att vara fullständigt städat. I ett stökigt rum spelar det ingen roll om en viss bok står till höger eller vänster i bokhyllan; rummet är i alla fall lika stökigt. Rummets entropi är antalet sätt man kan ställa saker för att uppnå en viss stökighetsnivå. Ju stökigare rummet är, desto fler ställen kan de ligga på och desto högre entropi får rummet. Det finns emellertid ingen helt allmängiltig vardagsspråksdefinition på entropi, mycket beroende på oklarheter angående begreppet "ordning"; i vissa speciella fall innebär ökad entropi att ordning och komplexitet kan uppkomma ur oordning. Strikt matematiskt sett är entropi en fråga om sannolikhetsgrader. Det stökiga rummet befinner sig i ett mer sannolikt tillstånd än det städade.

Entropi introducerades som en termodynamisk tillståndsfunktion av Rudolf Clausius år 1865. Inom termodynamiken kan entropi användas för att beskriva hur förändringen hos atomer, molekyler, gaser, värmeflöden och så vidare strävar mot energimässig utjämning, eller mest sannolika (energi)tillstånd. Entropin kan här sägas vara ett sätt att beskriva mängden energi som är tillgänglig för arbete. Ju större potential till förändring (låg entropi) som frigörs och kan tas tillvara i en process, desto större arbete kan utföras. Det totala resultatet av processen blir alltid högre entropi.

Innehåll 1 Definition 1.1 Mikroskopisk definition 1.2 Makroskopisk definition 2 Se även 3 Källor

Definition

Entropi har två olika defintioner, en mikroskopisk och en makroskopisk. Dessa två definitioner är likvärdiga, men förekommer i olika tillämpningar.

Mikroskopisk definition

I den mikroskopiska defintionen, som används inom statistisk mekanik, mäter entropin oordningen hos varje individuell frihetsgrad, det vill säga variationen av mikrotillstånd. Den totala entropin är summan av varje entropibidrag från respektive frihetsgrad, exempelvis vibrationsfrekvens, magnetiskt bidrag, och dylikt. Betecknas ofta med bokstaven S. Termodynamikens andra huvudsats säger att naturens riktning är att öka oordningen, vilket oftast postuleras som att jämvikt uppstår då entropin uppnått sitt maximala värde.

Den generella entropidefinitionen är

där k är Boltzmanns konstant och

är sannolikheten att systemet är i tillstånd r med energin U_r, för en viss frihetsgrad r.

Detta är ekvivalent med Boltzmanns entropidefinition för ett system i jämvikt:

där Ω är den antalet mikrotillstånd. U är systemets inre energi, V systemets volym och N antal partiklar i volymen.

Makroskopisk definition

I den makroskopiska definitionen, som används inom den klassiska termodynamiken definieras entropi genom

så att dS är entropiändringen vid en reversibel tillsats av värmemängden dq. Eftersom den reversibla vägen mellan två tillstånd är den väg som ger det största arbetet, ger denna definition tillsammans med termodynamikens första huvudsats att

vilket är Clausius olikhet, dvs en matematisk formulering av termodynamikens andra huvudsats.

Med argument från den statistiska mekaniken kan temperaturen definieras som

Eftersom dU = dq vid konstant volym indikerar detta att Boltzmanns definition och den termodynamiska definitionen av entropi är ekvivalenta.

Se även

• Termodynamik

Källor

1. ↑ Mandl, F: Statistical Physics, Jown Wiley & Sons, Ltd, Chichester, England 1999, sid. 34. ISBN 0-471-91533-5.