Hermites rotansats

Från Rilpedia

Texten från svenska Wikipedia

Hermites rotansats är en metod i matematik uppkallad efter Charles Hermite. Metoden kan användas för att enkelt bestämma en primitiv funktion till speciella uttryck med rötter, specifikt uttryck som uppfyller att integranden är en kvot mellan ett polynom och roten ur ett andragradspolynom.

Sats

Om $P$ är ett polynom av grad 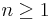$n \ge 1$ , så finns ett polynom $Q$ av grad $n - 1$ och en konstant $K$ så att

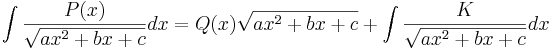
$\int\frac{P(x)}{\sqrt{ax^2+bx+c}}dx=Q(x)\sqrt{ax^2+bx+c}+\int\frac{K}{\sqrt{ax^2+bx+c}}dx$

Allmänt exempel

För att använda satsen börjar man naturligtvis med att försäkra sig om att uttrycket uppfyller kraven, och så noterar man gradtalet på $P (x)$ . Sedan ansätter man helt enkelt ett polynom $Q$ av lägre grad, dvs.

$Q (x) = B 0 + B 1 x + ... + B n - 1 x n - 1$ .

Detta ger då att

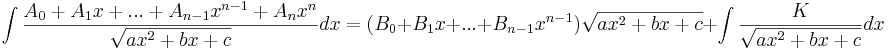
$\int\frac{A_0+A_1x+...+A_{n-1}x^{n-1}+A_nx^n}{\sqrt{ax^2+bx+c}}dx =(B_0+B_1x+...+B_{n-1}x^{n-1})\sqrt{ax^2+bx+c}+\int \frac{K}{\sqrt{ax^2+bx+c}}dx$

Nästa steg blir sedan att derivera båda sidor i likheten. De obestämda integralerna blir särskilt enkla att derivera, då det bara är integranden som blir kvar. I övrigt används vanliga deriveringsregler. Slutligen sätter man hela högerledet på gemensam nämnare, så att nämnaren stämmer överens med den i vänsterledet.

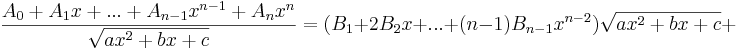
$\frac{A_0+A_1x+...+A_{n-1}x^{n-1}+A_nx^n}{\sqrt{ax^2+bx+c}} =(B_1+2B_2x+...+(n-1)B_{n-1}x^{n-2})\sqrt{ax^2+bx+c} +$

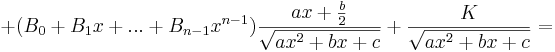
$+ (B_0+B_1x+...+B_{n-1}x^{n-1})\frac{ax+\frac{b}{2}}{\sqrt{ax^2+bx+c}} +\frac{K}{\sqrt{ax^2+bx+c}}=$

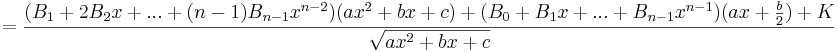
$=\frac{(B_1+2B_2x+...+(n-1)B_{n-1}x^{n-2})(ax^2+bx+c)+(B_0+B_1x+...+B_{n-1}x^{n-1})(ax+\frac{b}{2})+K}{\sqrt{ax^2+bx+c}}$

Härifrån är det bara att identifiera och lösa ut koefficienterna i täljaren, för att slutligen stoppa in i ansatsen.

Det enda som sedan återstår är att beräkna den högra integralen, men eftersom K är en konstant görs detta enkelt enligt följande

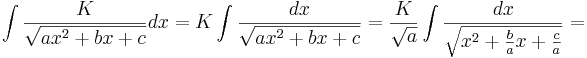
$\int\frac{K}{\sqrt{ax^2+bx+c}}dx=K\int\frac{dx}{\sqrt{ax^2+bx+c}}=\frac{K}{\sqrt{a}}\int\frac{dx}{\sqrt{x^2+\frac{b}{a}x+\frac{c}{a}}}=$

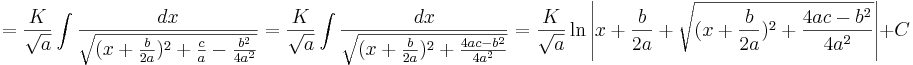
$=\frac{K}{\sqrt{a}}\int\frac{dx}{\sqrt{(x+\frac{b}{2a})^2+\frac{c}{a}-\frac{b^2}{4a^2}}} =\frac{K}{\sqrt{a}}\int\frac{dx}{\sqrt{(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a^2}}} =\frac{K}{\sqrt{a}}\ln\left|x+\frac{b}{2a}+\sqrt{(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a^2}}\right|+C$

Där vi i slutsteget har använt följande standardintegral

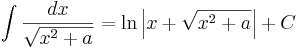$\int\frac{dx}{\sqrt{x^2+a}}=\ln\left|x+\sqrt{x^2+a}\right|+C$ då $a \neq 0$

Exempel på användning

Vi ska nu använda Hermites Rot-ansats för att ta fram följande primitiva funktion. Exemplet är hämtat ur "Matematisk analys en variabel" av Göran Forsling och Mats Neymark på Linköpings Universitet.

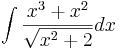
$\int\frac{x^3+x^2}{\sqrt{x^2+2}}dx$

Vi börjar med att konstatera att den uppfyller våra tidigare ställda krav, och att gradtalet på täljarens polynom är tre. Vi ansätter därför ett polynom av grad två, $Q (x) = A x 2 + B x + C$ och enligt Hermites rotansats så gäller

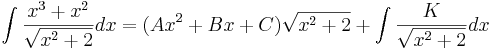$\int\frac{x^3+x^2}{\sqrt{x^2+2}}dx=(Ax^2+Bx+C)\sqrt{x^2+2}+\int\frac{K}{\sqrt{x^2+2}}dx$ där A, B, C och K är konstanter.

Derivering av VL och HL ger

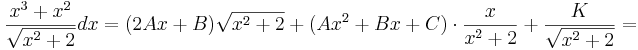
$\frac{x^3+x^2}{\sqrt{x^2+2}}dx=(2Ax+B)\sqrt{x^2+2}+(Ax^2+Bx+C)\cdot\frac{x}{x^2+2}+\frac{K}{\sqrt{x^2+2}}=$

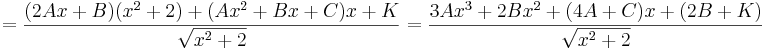
$=\frac{(2Ax+B)(x^2+2)+(Ax^2+Bx+C)x+K}{\sqrt{x^2+2}}=\frac{3Ax^3+2Bx^2+(4A+C)x+(2B+K)}{\sqrt{x^2+2}}$

Identifiering av koefficienterna ger följande ekvationssystem

$\begin{cases} 3A = 1\\ 2B = 1\\ 4A + C = 0\\ 2B + K = 0 \end{cases}\mbox{Vilket ger att } \begin{cases} A = \frac{1}{3}\\ B = \frac{1}{2}\\ C = -\frac{4}{3}\\ K = -1 \end{cases}$

Detta insatt i ursprungsansatsen ger

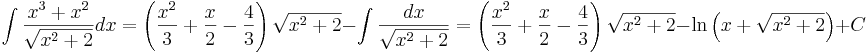
$\int\frac{x^3+x^2}{\sqrt{x^2+2}}dx=\left(\frac{x^2}{3}+\frac{x}{2}-\frac{4}{3}\right)\sqrt{x^2+2}-\int\frac{dx}{\sqrt{x^2+2}} =\left(\frac{x^2}{3}+\frac{x}{2}-\frac{4}{3}\right)\sqrt{x^2+2}-\ln\left(x+\sqrt{x^2+2}\right)+C$

Referenser

Forsling, Göran och Neymark, Mats, Matematisk analys en variabel, (2004), Liber ISBN 9147051884

Hermites rotansats

Från Rilpedia

Innehåll

Sats

Allmänt exempel

Exempel på användning

Referenser

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda