Heine-Borels sats
Från Rilpedia
Heine-Borels sats är en matematisk sats om kompakta mängder uppkallad efter Eduard Heine och Émile Borel.
Heine-Borels sats har två formuleringar; en för ändligtdimensionella 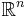 -rum och en för allmänna metriska rum. Den första formuleringen säger att:
-rum och en för allmänna metriska rum. Den första formuleringen säger att:
- En delmängd
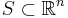 är kompakt om och endast om S är sluten och begränsad.
är kompakt om och endast om S är sluten och begränsad.
Inom reell analys används ibland den andra delen av satsen som defintionen på kompakt mängd, men i allmänna metriska rum gäller bara att kompakhet implicerar slutenhet och begränsning. Det finns istället en allmännare form av Heine-Borels sats:
- En delmängd till ett metriskt rum är kompakt om och endast om rummet är fullständigt och mängden sluten och totalt begränsad.
Innehåll |
Bevis
Bevis av den första formuleringen; 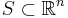 kompakt omm S sluten och begränsad. Implikationen att kompakthet ger slutenhet och begräsning visas för metriska rum. Kom ihåg defintionen för kompakt mängd; att varje öppen övertäckning av mängden har en ändlig delövertäckning som täcker mängden.
kompakt omm S sluten och begränsad. Implikationen att kompakthet ger slutenhet och begräsning visas för metriska rum. Kom ihåg defintionen för kompakt mängd; att varje öppen övertäckning av mängden har en ändlig delövertäckning som täcker mängden.
Kompakthet ger slutenhet
Låt  (komplementet till S). För alla
(komplementet till S). För alla 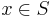 existerar disjunkta omgivningar Bx som innehåller x och
existerar disjunkta omgivningar Bx som innehåller x och 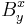 som innehåller y. Det följer att alla Bx-mängder bildar en öppen övertäckning av S,
som innehåller y. Det följer att alla Bx-mängder bildar en öppen övertäckning av S,  . S är kompakt, så det existerar en ändlig delövertäckning som täcker S av mängder
. S är kompakt, så det existerar en ändlig delövertäckning som täcker S av mängder  , så att
, så att 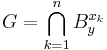 är en omgivning till y som inte ligger i S, så y kan inte vara en hopningspunkt till S. Då y valdes godtyckligt ger detta att S innehåller alla sina hopningspunkter och är därmed sluten.
är en omgivning till y som inte ligger i S, så y kan inte vara en hopningspunkt till S. Då y valdes godtyckligt ger detta att S innehåller alla sina hopningspunkter och är därmed sluten.
Kompakthet ger begränsning
I allmänna metriska rum innebär att en mängd är begränsad 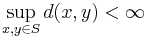 där d är metriken på S. En öppen övertäckning till S är mängden av klot med radie 1 med mittpunkt i x, betecknad B1(x) för alla x i S. Denna övertäckning har då en ändlig delövertäckning B1(x1),...,B1(xN) som täcker S. Antag att
där d är metriken på S. En öppen övertäckning till S är mängden av klot med radie 1 med mittpunkt i x, betecknad B1(x) för alla x i S. Denna övertäckning har då en ändlig delövertäckning B1(x1),...,B1(xN) som täcker S. Antag att  och
och  och
och  , som
, som
då x och y valdes godtyckligt ger detta att S är begränsad.
Slutenhet och begräsning ger kompakthet
Om en mängd 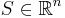 är begränsad kan den stängas in i en n-låda:
är begränsad kan den stängas in i en n-låda:
med ak < bk och 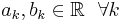 . Kalla denna n-låda för T0. Man kan nu dela upp T0 i flera små dellådor genom att dela varje sida i två. Vi får då 2n dellådor.
. Kalla denna n-låda för T0. Man kan nu dela upp T0 i flera små dellådor genom att dela varje sida i två. Vi får då 2n dellådor.
Antag att T0 inte är kompakt, då givet en öppen övertäckning C av T0 måste finnas minst en dellåda till T0 som kräver oändligt många öppna mängder för att täckas, kalla denna låda T1. Fortsätt sedan med samma resonemang, dela upp T1 i 2n dellådor och plocka ut T2, osv. Man får då en följd av T-mängder
vars längd, projicerat på xj-axeln, går mot noll då n går mot oändligheten:
Då ger Cantors inkapslingssats: 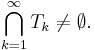 , dvs det finns en punkt
, dvs det finns en punkt 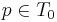 . Eftersom C täcker S finns en mängd
. Eftersom C täcker S finns en mängd 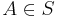 så att
så att 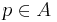 . Då A är öppen finns ett n-klot
. Då A är öppen finns ett n-klot 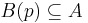 , så att för tillräckligt stora k gäller
, så att för tillräckligt stora k gäller  , så att de oändligt många mängderna som behövs för att täcka Tk kan ersättas med endast en, vilket ger en motsägelse. Alltså är T0 kompakt.
, så att de oändligt många mängderna som behövs för att täcka Tk kan ersättas med endast en, vilket ger en motsägelse. Alltså är T0 kompakt.
S är alltså en sluten delmängd av en kompakt mängd, då resultatet nedan ger att S är kompakt.
Sluten delmängd till kompakt mängd är kompakt
Låt S vara en sluten delmängd till den kompakt mängden T i 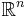 . Låt CS vara en öppen övertäckning av S. Om CS också täcker T så existerar det en ändlig delövertäckning av CS som täcker T, anta därför att CS inte täcker T.
. Låt CS vara en öppen övertäckning av S. Om CS också täcker T så existerar det en ändlig delövertäckning av CS som täcker T, anta därför att CS inte täcker T.
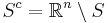 är då en öppen mängd som innehåller punkter i T som inte täcks av CS. Låt
är då en öppen mängd som innehåller punkter i T som inte täcks av CS. Låt 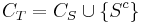 vara en öppen övertäckning av T. Eftersom T är kompakt så har CT' en ändlig delövertäckning. Då Sc innehåller punkter i T som inte täcks av CS måste
vara en öppen övertäckning av T. Eftersom T är kompakt så har CT' en ändlig delövertäckning. Då Sc innehåller punkter i T som inte täcks av CS måste 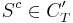 , så att
, så att 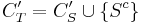 , där CS' måste vara en ändlig delövertäckning av CS eftersom Sc inte täcker S så
, där CS' måste vara en ändlig delövertäckning av CS eftersom Sc inte täcker S så 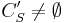 .
.




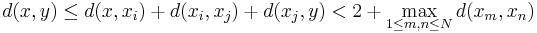
![S \subseteq [a_1, b_1] \times [a_2, b_2] \times ... \times [a_n, b_n]](/w/images/sv.rilpedia.org/math/5/6/3/5630343ff902ef849032bed35afaf20d.png)