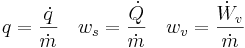Energiekvationen
Från Rilpedia
Energiekvationen bygger på Reynolds transportteorem (RTT) där den extensiva storheten B står för energi. Den intensiva storheten β blir då energi per enhet massa:
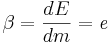
Innehåll |
Grundform
Energiekvationen kan förenklas beroende på förhållanden men skrivs i grundform som:
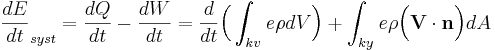
där Q står för värme, W för arbete (alltså står 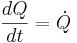 för överfört värme per tidsenhet och
för överfört värme per tidsenhet och 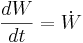 för arbete per tidsenhet), kv för kontrollvolym och ky för kontrollyta. V är en hastighetsvektor och n är en enhetsvektor (negativ för inflöde och positiv för utflöde). e är summan av:
för arbete per tidsenhet), kv för kontrollvolym och ky för kontrollyta. V är en hastighetsvektor och n är en enhetsvektor (negativ för inflöde och positiv för utflöde). e är summan av:
e = eintern + ekinetisk + epotentiell + eannan
Den sista termen övrig rör kemiska eller nukleära reaktioner alternativt magnetfält och är därför nästan alltid lika med noll. e kan då skrivas om med 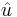 som intern energi och längden z ritkad uppåt:
som intern energi och längden z ritkad uppåt:
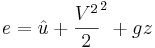
Arbete per tidsenhet består av axelarbetet 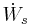 , de viskösa spänningarnas arbete
, de viskösa spänningarnas arbete 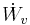 samt tryckkrafternas arbete
samt tryckkrafternas arbete 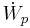 . De två senare är:
. De två senare är:
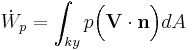
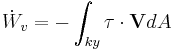
Där p är trycket i fluiden och 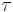 är spänningsvekorn. Alltså är arbetet (notera att de viskösa spänningarnas arbete är negativt):
är spänningsvekorn. Alltså är arbetet (notera att de viskösa spänningarnas arbete är negativt):
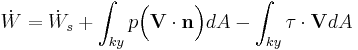
Energiekvationen kan då skrivas om till:
![\dot Q - \dot{W}_s - \dot{W}_v = {d \over dt} \Bigg[ \int_{kv} \Big( \hat{u} + {V^2 \over 2} + gz \Big) \rho dV \Bigg] + \int_{ky} \Big( \hat{h} + {V^2 \over 2} + gz \Big) \rho \Big( \mathbf{V} \cdot \mathbf{n} \Big) dA](/w/images/sv.rilpedia.org/math/4/a/7/4a745c0815fa5e4af067f871abf0527c.png)
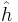 står för entalpi och definieras som
står för entalpi och definieras som 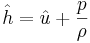 .
.
Endimensionellt in- och utflöde
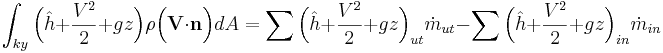
Stationär strömning, ett endimensionellt inlopp samt ett endimensionellt utlopp
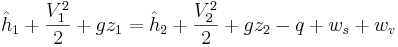
där