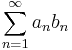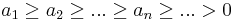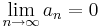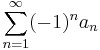Dirichlets test
Från Rilpedia
Dirichlets test är inom matematik en metod för att testa om en serie konvergerar uppkallad efter matematikern Dirichlet.
Givet två följder av reella tal, (an) och (bn), konvergerar serien
om (an) och (bn) uppfyller:
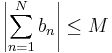 för varje naturligt tal N.
för varje naturligt tal N.
En följd av Diriclets test är Leibniz kriterium, som säger att serien
konvergerar om följden (an) är minskande mot noll. Följden (bn) är i det här fallet bn = ( − 1)n vars serie uppenbart är begränsad av talet 1.