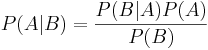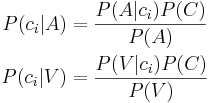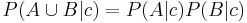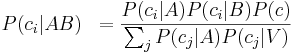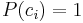Den perceptuella fuzzy-logic-modellen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Den perceptuella fuzzy-logic-modellen (Fuzzy-logical model of perception, FLMP) är en

perceptionsmodell, utarbetad av Dominic Massaro verksam vid University of California, Santa Cruz. FLMP kan tillämpas inom många områden, däribland multimodal talperception. I vardagligt tal är talpercetion en audiovisuell process där lyssnaren, förutom ljud, även har tillgång till visuell information från talarens ansikte och dennes talgester. Det är uppenbart att den visuella signalen underlättar förståelsen i bullriga miljöer. Men den visuella signalen påverkar det vi hör, även då den akustiska signalen inte är störd av brus. Ett exempel på detta är McGurk-effekten: Ett ansikte som till synes uttalar [gaga], då den akustiska signalen är utbytt mot [baba] percipieras som [dada] av en överväldigande majoritet. Perceptet är i och med detta en sammansmältning av informationen från de båda modaliteterna.

Enligt FLMP sker perceptionen i tre steg: Evaluering, Integration och Avgörande.


Innehåll

Evaluering

Det första steget innebär att informationen evalueras i de båda modaliteterna (den auditiva och den visuella) var för sig. Evalueringen innebär att den inkommande signalen matchas mot lagrade prototyper av möjliga responser. Signalens förhållande till var och en av prototyperna registreras som graderat sanningsvärde på en skala 0 till 1. Till skillnad från sannolikheter kan summan av de olika graderna av sanningsvärde för de olika prototyperna överstiga 1.


Integration

FLMP utgår från Baysiansk integration. Trots att Bayes sats opererar på sannolikheter, tillämpas den här istället på graderat sanningsvärde.

Bayes sats säger att:


\begin{align} P(A|B) & = \frac{P(B | A) P(A)}{P(B)} \end{align}

Dvs. sannolikheten för A betingat B är lika med sannolikheten för att B betingat A, multiplicerat med sannolikheten för A, delat med sannolikheten för B.

I termer av sannolikhet för percipierat språkljud ci, givet den akustiska evidensen A och den visuella evidensen V får vi:

\begin{align} P(c_i|A) & = \frac{P(A | c_i) P(C)}{P(A)} \\ P(c_i|V) & = \frac{P(V | c_i) P(C)}{P(V)} \end{align}

Sannolikheten för två händelser, A och B, är detsamma som produkten av dessa händelser för sig, givet att de är oberoende:

\begin{align} P(A \cup B |c) & = P(A | c) P(B | c) \end{align}

Detta ger följande responssannolikheter för språkljudet ci:

\begin{align} P(c_i | A & B) & = \frac{P(c_i | A) P(c_i | B)P(c)}{\sum_{j}{P(c_j|A)P(c_j|V)}} \end{align}

Eftersom språkljudskategorin ci existerar:

\begin{align} P(c_i) = 1 \end{align}


Avgörande

Det slutgiltiga perceptet bygger på de baysianska responssannolikheterna för var och en av de tänkbara percepten. Dessa räknades ut i det tidigare steget. En viktig detalj är att perceptet enligt FLMP är amodalt. På denna punkt skiljer sig modellen från gestuella och auditiva talperceptionsteorier.

Källor

  • Massaro W.M. & Stork D.G., Speech Recognition and Sensory integration (1998) American Scientist. 86. sid. 236-244.
  • McGurk H. & MacDonald J., Hearing lips and seeing voices (1976) Nature. 264. sid. 746-748.
  • Sumby, W.H. & I. Pollack, Visual contribution to speech intelligibility in noise (1954) Journal of the Acoustical Society of America. 26. sid. 212-215.
Hämtad från "https://sv.rilpedia.org/wiki/Den_perceptuella_fuzzy-logic-modellen"
Personliga verktyg