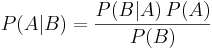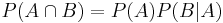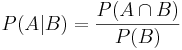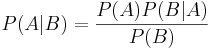Från Rilpedia

Bayes sats eller Bayes teorem är en sats inom sannolikhetsteorin som används för att bestämma sannolikheten för ett utfall givet ett annat utfall. Satsen har fått sitt namn av matematikern Thomas Bayes.

Bayes sats

Sannolikheten P för A givet B kan skrivas som:

där

• P(A | B) är den betingade sannolikheten för A om B är givet.
• P(B | A) är den betingade sannolikheten för B givet A.
• P(A) och P(B) är sannolikheten för A respektive B.

Tillämpningar

Bayes sats används flitigt inom statistiken, bland annat för dolda Markovmodeller. Satsen och Bayes namn har blivit smått berömd i interneteran genom att den har implementerats i Bayesiska skräppostfilter för att på ett statistiskt sätt kunna separera skräp-e-post från önskad e-post.

Härledning

Från formeln för betingad sannolikhet får man:

man får även:

använd uttrycket för 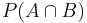från första uttrycket i andra uttrycket, då man får:

vilket är Bayes sats.