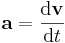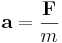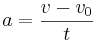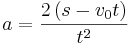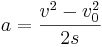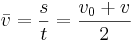Acceleration
Från Rilpedia
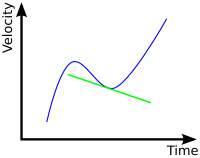
Acceleration är en fysikalisk storhet som anger förändring av hastighet per tidsenhet. Förändringen kan vara såväl positiv (ökad hastighet) som negativ (minskad hastighet) eller innebära en ändrad riktning. Vid retardation (deceleration, inbromsning) är accelerationen negativ och hastighetens belopp minskar således. Vid acceleration ortogonalt mot rörelseriktningen fås en krökt bana utan förändring av hastighet eller rörelseenergi. Om accelerationen i sidled är konstant blir banan en cirkel. SI-enheten för acceleration är m/s2.
Innehåll |
Historia
Begreppet acceleration formaliserades av Pierre Varignon (1654-1722) den 20 januari 1700 som en oändligt liten skillnad i hastighet i tiden vid en oändligt liten tidsskillnad. Begreppet bygger på den teori Leibniz (1646-1716) utvecklat två år tidigare.
Exempel
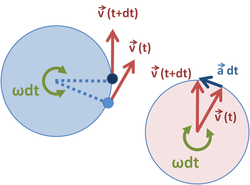
En bil som startar från stillastående och accelererar rakt fram har en acceleration vars riktning sammanfaller med dess hastighet och hastigheten ökar. När accelerationen minskar till noll avtar hastighetsökningen och bilen får en konstant fart framåt. Om nu vägen svänger men bilens hastighet längs vägen är densamma, hastighetsmätaren visar konstant hastighet, så kommer ändå hastighetens riktning att variera. För att detta skall ske krävs en acceleration i sidled. Då vägen och bilen svänger till vänster är accelerationen således riktad rakt åt vänster relativt bilen, och tvärtom vid en högersväng. Den acceleration i sidled som behövs beror på vägens krökning, en skarpare kurva, eller del av kurva, kräver en större acceleration i sidled. Låt oss sedan anta att bilen, fortfarande med konstant hastighet längs vägen, når en raksträcka igen. Då återgår dess acceleration till noll. Om sedan bilen skall stanna längs raksträckan, bromsar föraren och generar en acceleration som är parallell med bilens hastighet men motriktad, och bilens hastighet minskar, eller annorlunda uttryckt, bilen retarderar.
Notera att vi i detta exempel inte gjort några antaganden om hur bilens acceleration uppkommer. På verkliga bilar uppstår accelerationer genom de krafter som verkar på bilens däck från marken och bilens motor, samt krafter från den omgivande luften och gravitationskrafter från det gravitationsfält bilen befinner sig i.
Ett annat praktiskt exempel på acceleration i sidled är omloppsbanor som den månen beskriver kring Jorden. Månen har en hastighet framåt men påverkas hela tiden av Jordens tyngdacceleration som verkar ortogonalt mot månens bana. Det gör att månens hastighet framåt hela tiden förändras så att månen i praktiken kretsar kring Jorden.
Beteckningar
Acceleration betecknas vanligen a.
Vid analys i mer än en dimension, vilket är vanligt inom till exempel mekanik och fältteori, behandlas då lämpligen acceleration som ett vektormått med beteckningen 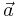 eller
eller 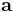 .
.
Accelerationens SI-enhet är m / s2 som läses "meter per sekundkvadrat".
En vanlig acceleration är tyngdaccelerationen som accelererar allting mot Jordens centrum. Denna acceleration förekommer så ofta i beräkningar att den brukar betecknas med en egen bokstav, 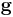 . När man vid rymdfärder, kollisioner och liknande pratar om ett visst antal
. När man vid rymdfärder, kollisioner och liknande pratar om ett visst antal 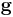 som uppnåtts anger man alltså en multipel till tyngdaccelerationen. En människa med massan 100 kg som utsätts för 3
som uppnåtts anger man alltså en multipel till tyngdaccelerationen. En människa med massan 100 kg som utsätts för 3 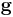 upplever således att han/hon väger 300 kg.
upplever således att han/hon väger 300 kg.
Härledningar
Acceleration definieras som tidsderivatan av hastigheten:
där a är accelerationen, v hastigheten och t tiden.
Acceleration är alltså förändringen av hastighet per tidsenhet. Vidare är hastighet derivatan av sträckan som funktion av tiden. Således är acceleration andraderivatan av sträckan.[1]
Notera att både hastighet och acceleration är egenskaper som definieras relativt en viss referensram. För bilen i exemplet ovan är en naturlig referensram den omgivning i vilken vägen ligger. För andra system är möjligen flera referensramar av intresse. För en raket vars mål är månen kommer hastighet och acceleration relativt både jorden och månen att vara av intresse, åtminstone i olika faser av resan. Foucaults pendel är ett annat exempel på ett system där flera referensramar är av betydelse. För att förutsäga dess rörelse några få svängningar är det tillräckligt med att betrakta jorden som en lämplig referensram, men för att förstå rörelsen under en längre tid krävs att en bättre lämpad referensram används, exempelvis en där jordens masscentrum är fixt tillsammans med riktningarna mot några fixstjärnor. I ännu knepigare fall kan krävas att solsystemets masscentrum och några lämpliga riktningar anses fixa, eller rentav Vintergatans masscentrum och riktningarna till några andra lämpliga galaxer.
Förhållandet mellan acceleration och kraft
Newtons rörelselagar beskriver förhållandet mellan acceleration och kraft (om massan är konstant):
där a är accelerationen, F är summan av alla krafter och m är massan.
Ovanstående ger att accelerationen är proportionell mot kraften och omvänt proportionell mot massan på det accelererade föremålet.
Formler för medelaccelerationen vid likformig rörelse
För att kunna beräkna medelaccelerationen använder man sig vanligen av fyra olika formler som man sedan kan skriva om och/eller använda tillsammans. Vilken som används beror på vilka variabler man känner till från början. I formlerna nedan står a för acceleration, v för den slutliga hastigheten som uppnåtts, v0 för begynnelsehastigheten, t för tiden och s för den sträcka som tillryggalagts.[2]
Formel man använder när starthastighet, sluthastighet och tid är kända.
När sträcka, tid och starthastighet är kända kan denna formel användas.
Denna formel används när man känner starthastighet, sluthastighet och sträcka.
I vissa fall kan man även behöva följande formel för att beräkna en variabel man saknar.
Se även
Källor
- ↑ Matematisk analys - en variabel av Göran Forsling och Mats Neymark, ISBN 91-47-05188-4, sida 218.
- ↑ Tabeller och formler för NV- och TE-Programmen av Ekbom m.fl, ISBN 91-47-01746-5, sida 98.
- Denna artikel är helt eller delvis baserad på material från franskspråkiga Wikipedia, Accélération, 21 december 2008.
Externa länkar
- Rörelse med konstant acceleration - En webbplats med accelerationsexperiment (svenska).
- Acceleration and Free Fall - Ett kapitel från en Internetbok (engelska).
- Science aid: Movement - En webbplats om fysikalisk rörelse (engelska).
- Science.dirbix: Acceleration - En webbplats om acceleration (engelska).
- Acceleration Calculator - En webbplats för att beräkna acceleration (engelska).
- Motion Characteristics for Circular Motion - En webbplats om cirkulär rörelse (engelska).
- Practical Guide to Accelerometers