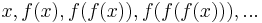Fixpunkt (matematik)
Från Rilpedia
Inom matematiken är en fixpunkt till en funktion en punkt som avbildas på sig själv, dvs en punkt a sådan att f(a) = a är en fixpunkt till f(x).
För att hitta fixpunkter till en funktion f(x) kan man lösa ekvationen f(x) = x.
Alla funktioner har inte fixpunkter, exempelvis y = f(x) = x − 1 fixpunktslös. I det här fallet ser man att funktionen beskriver en linje som är parallell med linjen y = x, och de kommer därför aldrig mötas.
Attraktiva fixpunkter
En attraktiv fixpunkt till en funktion f är punkt x0 sådan att för varje x i definitionsmängden till f som är tillräckligt nära x0 så konvergerar serien:
till x0.
Cosinus har en fixpunkt och den är attraktiv. "Tillräckligt nära" i det här fallet innebär alla reella tal. Serien kommer för cosinus att konvergera mot ungefär 0,73909. Dock är inte alla fixpunkter är inte attraktiva, t.ex. så har funktionen f(x) = 2x en fixpunkt i x0 = 0, men i alla närheter av x0 (förutom just i x0) kommer funktionen att avlägsna sig från x0 istället för att närma sig.
En fixpunkt x0 är garanterat attraktivt om f är kontinuerligt deriverbar i en omgivning till x0 och 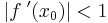 ,
,
Fixpunktssatser
Det finns många fixpunktssater som garanterar att det finns en fixpunkt till en funktion under vissa omständigheter. Exempelvis Brouwers fixpunktssats och Borels fixpunktssats