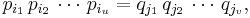Aritmetikens fundamentalsats
Från Rilpedia
Aritmetikens fundamentalsats är ett teorem inom matematik; mer specifikt inom den gren av matematik som kallas talteori. Satsen säger att de positiva heltalen (det vill säga talen 1,2,3,...) är "uppbyggda" av de så kallade primtalen:
- Varje positivt heltal kan skrivas som en produkt av primtal på precis ett sätt.
Frasen "på precis ett sätt" innebär att det finns endast en uppsättning primtal som ger det givna heltalet; så är exempelvis talet 6 "uppbyggt" av de två primtalen 2 och 3: 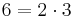 , men även
, men även 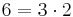 ; man gör ingen skillnad på de två produkterna
; man gör ingen skillnad på de två produkterna 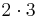 och
och 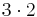 .
.
Innehåll |
Bevis för existensen av en primtalsfaktorisering
För detta bevis räknar vi talet 1 som ett primtal.
Beteckna med symbolen A mängden av alla positiva heltal som kan skrivas som en produkt av primtal; denna mängd är icke-tom då den exempelvis innehåller talet 42. Vi skall visa att mängden A innehåller alla positiva heltal och väljer att visa detta med ett så kallat motsägelsebevis (Latin: reductio ad absurdum).
- Antag därför att A inte är lika med mängden av alla positiva heltal.
Då finns det positiva heltal som ligger utanför mängen A, det vill säga positiva heltal som inte kan skrivas som en produkt av primtal. Samla alla sådana tal i en egen mängd och beteckna den med symbolen B. Välordningsaxiomet för de positiva heltalen säger att:
- "Varje icke-tom mängd av positiva heltal innehåller ett minsta element."
Därför innehåller mängden B ett minsta element, som vi betecknar med symbolen m.
Varje positivt heltal är antingen ett primtal eller så är det inte ett primtal; om det inte är ett primtal så kan det skrivas som en produkt av två mindre positiva heltal. Vi skall nu reda ut konsekvenserna av detta för heltalet m.
- Om talet m är ett primtal så kan det inte skrivas som en produkt av primtal, eftersom m är ett element i mängden B. Men detta är en motsägelse, eftersom både talen m och 1 är primtal, och m kan skrivas som en produkt av två primtal, nämligen
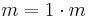 .
. - Om talet m inte är ett primtal så kan det skrivas som en produkt av två mindre positiva heltal p och q. Talet p är antingen ett element i mängden B, eller så är det inte det.
- Om p är ett element i mängden B, så får vi en motsägelse, eftersom p då är ett element i B som är mindre än det minsta elementet (m) i B.
- Om p inte är ett element i mängden B, så är det ett element i mängden A. Eftersom varje element i mängden A kan skrivas som en produkt av primtal, så kan talet p skrivas som en produkt av primtal.
- Samma resonemang som vi har fört om talet p kan vi även föra om talet q. Vi har därför kommit fram till slutsatsen att både talen p och q kan skrivas som produkter av primtal. Då kan även talet m skrivas som en produkt av primtal, eftersom
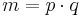 . Men detta är en motsägelse, eftersom vi vet att m inte kan skrivas som en produkt av primtal.
. Men detta är en motsägelse, eftersom vi vet att m inte kan skrivas som en produkt av primtal.
Vi ser att oavsett om m är ett primtal eller inte, så leds vi till en motsägelse. Detta innebär att det var fel av oss att anta att mängden A inte var lika med mängden av alla positiva heltal. Med andra ord har vi lyckats visa att varje positivt heltal kan skrivas som en produkt av primtal, vilket är vad vi ville bevisa.
Bevis för primtalsfaktoriseringens entydighet
Vi skall visa att varje positivt heltal kan framställas som en produkt av primtal på endast ett sätt; vi bortser från ordningen i den meningen att, exempelvis, 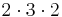 och
och 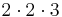 samt
samt 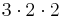 anses vara en och samma produkt. Vi väljer att bevisa satsen med ett motsägelsebevis.
anses vara en och samma produkt. Vi väljer att bevisa satsen med ett motsägelsebevis.
- Antag därför att det finns positiva heltal som kan framställas som en produkt av primtal på mer än ett sätt.
Låt n vara ett sådant positivt heltal och studera två framställningar av heltalet n som en produkt av primtal:
Vissa av p-primtalen kanske är identiska med q-primtalen; därför dividerar vi bort alla sådana primtal, vilket innebär att:
där p-primtalen och q-primtalen alla är olika. Om vi tillämpar nedanstående hjälpsats på primtalet 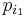 och produkten
och produkten 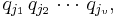 så kan vi hävda att primtalet
så kan vi hävda att primtalet 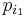 delar något av primtalen
delar något av primtalen 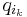 . Men detta är omöjligt, varför vi tvingas inse att:
. Men detta är omöjligt, varför vi tvingas inse att:
- Det var fel att anta att det fanns positiva heltal som kunde framställas som en produkt av primtal på mer än ett sätt.
Hjälpsats
Om p är ett primtal som delar en produkt av heltal,  , så delar primtalet minst en av faktorerna
, så delar primtalet minst en av faktorerna 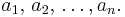
Bevis av hjälpsatsen
(VARNING: Det här beviset av hjälpsatsen är felaktigt. Se den engelska versionen av wikipedia istället, där Bézout's identity används för beviset! /g.eriksson)
Vi låter p vara ett primtal som delar en produkt av heltal,  , och vi antar att primtalet inte delar någon av faktorerna ai. Men då delar inte primtalet p produkten av faktorerna heller, vilket är en motsägelse.
, och vi antar att primtalet inte delar någon av faktorerna ai. Men då delar inte primtalet p produkten av faktorerna heller, vilket är en motsägelse.
Det var fel av oss att anta att primtalet inte delade någon av faktorerna ai. Därför delar primtalet p minst en av faktorerna, vilket är vad vi ville bevisa.