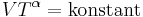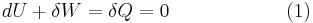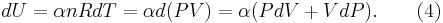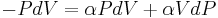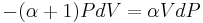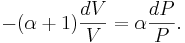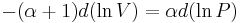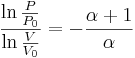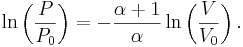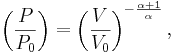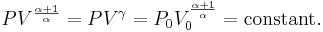Adiabatisk process
Från Rilpedia
En adiabatisk process är en termodynamisk process där ingen värme tillförs eller bortförs från en fluid. Ordet "adiabatisk" betyder i sig avsaknad av värmeöverföring, och används även till exempel för adiabatisk flamtemperatur, vilket är temperaturen en låga skulle nå om den inte förlorade värme till omgivningen. Om en adiabatisk process även är reversibel kallas den isentropisk.
Motsatsen, i vilken så mycket värme som möjligt överförs till och från omgivningen och leder till att temperaturen hålls konstant, kallas för en isotermisk process. Eftersom temperaturen är termodynamiskt konjugat till entropin så är isoterma processer konjugat till adiabatiska för reversibla processer. En process där ett visst värmeutbyte sker med omgivningen kallas för en polytrop process.
En process kan anses adiabatisk om den är snabb nog så att värmeöverföringen är minimal.
Innehåll |
Adiabatisk uppvärmning och kylning
Adiabatisk uppvärmning och kylning inträffar då trycket för en gas ändras. Adiabatisk uppvärmning sker när trycket ökar, vilket man bland annat kan notera för cykelpump. Efter att en sådan använts för att pumpa upp exempelvis en cykelslang kan man märka att pumpen blivit varmare på grund av adiabatisk uppvärmning. Dieselmotorer bygger på adiabatisk uppvärmning under kompressionsdelen av cykeln för att värma upp bränslet tillräckligt för att det skall kunna antändas.
Adiabatisk kylning sker istället när gasens tryck minskar, till exempel när den får expandera till en större volym. Detta kan man märka om man släpper ut luften ur ett däck; den utpysande luften kommer vara betydligt kallare än däcket, och när däcket är tomt kommer ventilen kännas kall. Adiabatisk kylning kräver inte en fluid; en teknik för att nå väldigt låga temperaturer (några få tusen- eller till och med miljondels kelvin över absoluta nollpunkten) är adiabatisk avmagnetisering, där förändringar i ett magnetfält används för att få till stånd adiabatisk avkylning.
Ideala gaser
För en klassisk ideal gas som undergår en adiabatisk process gäller att
där P är trycket, V volymen, och
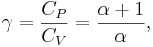 där
där
CP är specifika värmet per mol för konstant tryck och CV är specifika värmet per mol för konstant volym. α är antalet frihetsgrader delat med 2 (3/2 för monoatomiska gaser, 5/2 för diatomiska gaser). För en monoatomisk ideal gas är γ = 5 / 3, och för en diatomisk gas (som kväv- eller syrgas, som tillsammans utgör huvuddelen av all luft) är γ = 7 / 5.
Notera att ovanstående formel endast gäller klassiska ideala gaser, och alltså inte fermi- eller Bose-Einstein-gaser.
Vidare gäller för adiabatiska processer att
där T är temperaturen i kelvin, vilket även kan skrivas
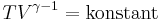 .
.
Härledning av 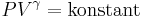
Definitionen för adiabatiska processer är att värmeöverföringen är noll, det vill säga δQ = 0. Enligt termodynamikens första lag gäller att
Där dU är förändringen i systemets inre energi och δW är det arbete utfört av systemet. Eftersom δQ=0 måste allt arbete ske på bekostnad av den inre energin. Arbetet δW gör definieras som
Dock kommer P inte förbli konstant utan förändras samtidigt som V.
Det som sökes är hur dP förhåller sig till dV under den adiabatiska processens fortlöpande. För en ideal gas ges den inre energin av
Där R är allmänna gaskonstanten och n är antalet mol i systemet (konstant).
Genom att differentiera ekvation (3) och använda ideala gaslagen fås
Vilket ofta skrivs som dU = nCVdT eftersom CV = αR.
Genom att infoga ekvationerna (2), (3) och (4) i ekvation (1) erhålles
vilket kan förenklas till
Genom att dividera båda led med PV fås
Vilket leder till att
vilket kan skrivas
För vissa konstanter P0 och V0 som fås ur det ursprungliga tillståndet. Vidare gäller
Genom att exponentiera båda led fås
vilket ger att
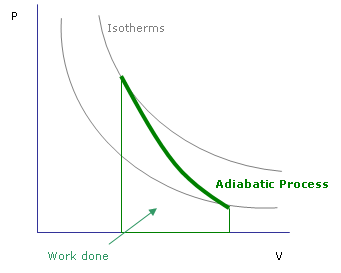
Adiabater i plottar
För adiabatiska linjer i ett P-V diagram gäller:
- Varje adiabat går asymptotiskt mot både V och P-axeln.
- Varje adiabat skär varje isoterm en och endast en gång.
Källor
- Denna artikel är helt eller delvis baserad på material från engelskspråkiga Wikipedia