Från Rilpedia

APL är en förkortning av "A Programming Language" och är ett tidigt programspråk ursprungligen utvecklat av Kenneth E. Iverson under dennes tid vid Harvard University och sedan vidareutvecklat av IBM.

APL togs från början fram främst som ett redskap för att beskriva datorer och algoritmer, d.v.s. i första hand inte som ett programspråk och användes huvudsakligen inom forskning. Notationen användes bl.a. för att beskriva arkitekturen för IBM System/360. Detta var en avsevärt mer exakt och detaljerad beskrivning än den dittills existerande dokumentationen och flera problem som tidigare inte uppmärksammats tydliggjordes. Iverson tilldelades 1979 års "Turing Award" för sitt arbete.

Innehåll 1 Historik 2 Översikt 3 Exempel 4 Referenser 5 Externa länkar

Historik

Iverson publicerade sin notation i en bok med titeln A programming Language 1962. 1964 implementerades en delmängd av notationen som ett programspråk. I början på 1980-talet presenterade IBM en avsevärt generaliserad och utvidgad version som man kallade APL2. Fram till senare halvan av 1980-talet var IBM sedan den dominerande leverantören av implementationer av APL. I början på 1990-talet skapade flera mindre företag konkurrerande versioner av språket, bl.a. APL2000 av STSC och Dyalog APL av Dyalog Ltd och dessa versioner har sedan på olika sätt vidareutvecklat språket.

Iverson konstruerade en efterföljare till APL kallat "J" som endast utnyttjar ASCII. Även andra språk erbjuder funktionalitet liknande APL. "A+" är ett öppen källkod-programspråk med många kommandon identiska med APL:s.

Översikt

APL har (och är ökänt för) en ovanlig, kraftfull och extremt kompakt syntax, starkt påverkad av matematisk notation. Koden konstrueras typiskt som en kedja av monadiska och dyadiska operatorer som verkar på mer eller mindre komplexa datastrukturer (arrayer). Deklarationer saknas i språket, och endast två sorters primitiva datatyper finns definierade, numeriska värden och text. APL var ett av de första programspråken (tillsammans med Lisp) som tillät rekursiva funktionsanrop, och p.g.a. de många och ovanliga operatorerna finns ingen definierad precedensordning mellan dessa. En kodrad interpreteras därför alltid från höger till vänster. Från början fanns inga kontrollstrukturer, som loopar, if-satser etc., definierade, utan behovet av dessa täcktes av speciella operatorer verkande på arrayer.

Språket är interpretativt, och programmeringen sker vanligtvis via en interaktiv dialog. APL använder en speciell teckenuppsättning och krävde från början ett speciellt tangentbord. Sedermera har det införts olika sätt att skriva APL-kod med utnyttjande av en vanlig ASCII-teckenuppsättning.

Skämtsamt har APL betecknats som ett "write-only"-språk vars kod var obegriplig även för den som skrivit den. Ibland gavs APL epitetet "A Problem Language" eller "Ape-Language". Ytterligare ett skämt-namn på 1970-talet var "Chinese BASIC", kanske för de många specialtecknen på tangentbordet, kanske för att APL i enklare programrader inte var svårare än BASIC. (Senare tillkom Chinese BASIC som namn på flera "riktiga" programspråk på kinesiska.)

Exempel

Följande APL-program hittar alla primtal från 2 till 10:

Detta är vad som händer (från höger till vänster):

1. Variabeln R tilldelas värdet 10 ( tilldelnings-primitiven )
2. En vektor med värdena från 1 till 10 skapas (funktionen ι)
3. Element nr 1 från vänster (händelsevis talet 1) i denna vektor tas bort (funktionen )
4. Den på så sätt reducerade vektorn tilldelas variabeln R. (tilldelnings-primitiven ). Observera att samma variabel kan tilldelas helt olika typer av data under programmets exekvering, i detta fallet först heltalet 10 och sedan vektorn (2,3,4,5,6,7,8,9,10)
5. Till vänster om R står reduktionsfunktionen, / , med ett parentesuttryck ytterligare till vänster.
6. Parentesen exekveras först. Beräkna ytterprodukten R multiplicerat med R, d.v.s. i detta fall en matris med 9 x 9 element där element_{i j} är R_i x R_j (ytterprodukts-funktionen 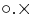skapas med operatorn 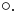applicerad på funktionen )
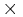7. Skapa en vektor med samma längd som vektorn R, där elementet är 1 om ett element i R återfinns i ytterprodukts-matrisen, annars 0. I detta fall vektorn (0,0,1,0,1,0,1,1,1). ( "ingår i"-funktion )
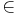8. Invertera denna vektor, d.v.s. byt 0 mot 1 och 1 mot 0 ( negerings-funktionen ˜ ). Parentesen innehåller nu en vektor med värdena (1,1,0,1,0,1,0,0,0).
9. Nu till reduktionsfunktionen / (pkt. 5 ovan). Välj ut de element ur vektorn R där motsvarande element i den nyss skapade vektorn är lika med 1. Vi får vektorn (2,3,5,7)
10. Skriv ut resultatet (automatisk funktion. Resultatet av varje rad i Ett APL-program skrivs ut om inte den sista operationen är tilldelnings-primitiven)

Referenser

• A programming Language, John Wiley and Sons Inc, 1962
• Programmera i APL, av J. Bohman och C-E. Fröberg, Studentlitteratur, 1976, ISBN 91-44-13161-5

Externa länkar

• A Formal Description of SYSTEM/360 (1964 artikel av Adin D. Falkoff, Kenneth E. Iverson, Edward H. Sussenguth)
• The Design of APL (1973 artikel av Adin D. Falkoff and Kenneth E. Iverson)
• A Personal view of APL av Kenneth E. Iverson
• Dyalog APL
• APL2000 (tidigare STSC, Manugistics)