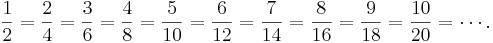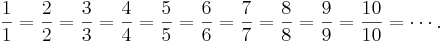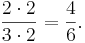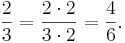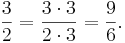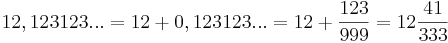Bråk
Från Rilpedia
I matematik är ett bråk ett tal, 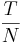 , som beskriver förhållandet mellan talet N och talet T. Talet T kallas för bråkets täljare (T som i tak) och talet N kallas för bråkets nämnare (N som i nere); för att ha något att jämföra med, förutsätter man att nämnaren inte är noll.
, som beskriver förhållandet mellan talet N och talet T. Talet T kallas för bråkets täljare (T som i tak) och talet N kallas för bråkets nämnare (N som i nere); för att ha något att jämföra med, förutsätter man att nämnaren inte är noll.
Den vågräta linjen mellan täljare och nämnare kallas bråkstreck. Tal som kan uttryckas som bråk kallas rationella tal.
Innehåll |
Exempel
Rough===När är två bråk likadana?=== Bråket 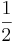 (Läs: En halv) talar om hur stort talet 2 är jämfört med talet 1: Dubbelt så stort.
(Läs: En halv) talar om hur stort talet 2 är jämfört med talet 1: Dubbelt så stort.
Bråket 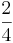 (Läs: Två fjärdedelar) talar om hur stort talet 4 är jämfört med talet 2: Dubbelt så stort.
(Läs: Två fjärdedelar) talar om hur stort talet 4 är jämfört med talet 2: Dubbelt så stort.
Bråket 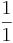 (Läs: En hel) talar om hur stort talet 1 är jämfört med talet 1: Lika stort.
(Läs: En hel) talar om hur stort talet 1 är jämfört med talet 1: Lika stort.
Bråket 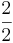 (Läs: Två halva) talar om hur stort talet 2 är jämfört med talet 2: Lika stort, men är hälften så stor i skalan.
(Läs: Två halva) talar om hur stort talet 2 är jämfört med talet 2: Lika stort, men är hälften så stor i skalan.
Detta visar att bråken 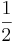 och
och 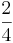 är samma, och att bråken
är samma, och att bråken 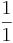 och
och 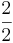 är samma:
är samma:
 täljare är nere
täljare är nere
Flera sätt att skriva ett bråk
Om nämnaren N är dubbelt så stor som täljaren T så är bråket 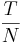 detsamma som bråket
detsamma som bråket 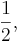 eftersom det bara talar om hur mycket större nämnaren är jämfört med täljaren; därför gäller det exempelvis att:
eftersom det bara talar om hur mycket större nämnaren är jämfört med täljaren; därför gäller det exempelvis att:
Om nämnaren N är lika stor som täljaren T så är bråket 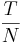 detsamma som bråket
detsamma som bråket 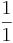 :
:
Gemensam nämnare
Är två bråk lika?
Är bråken 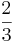 (Läs: Två tredjedelar) och
(Läs: Två tredjedelar) och  (Läs: Fyra sjättedelar) samma? Det är svårt att tala om hur mycket större talet 3 är jämfört med talet 2, men om vi förstorar dem lika mycket kommer förhållandet mellan dem inte att ändras: Om vi gör 2 dubbelt så stort och 3 dubbelt så stort, får vi bråket
(Läs: Fyra sjättedelar) samma? Det är svårt att tala om hur mycket större talet 3 är jämfört med talet 2, men om vi förstorar dem lika mycket kommer förhållandet mellan dem inte att ändras: Om vi gör 2 dubbelt så stort och 3 dubbelt så stort, får vi bråket
Detta visar att bråken 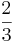 och
och  faktiskt är samma tal.
faktiskt är samma tal.
-
- När man vill jämföra två bråk skall man se till att deras nämnare är samma tal; i detta fall var den gemensamma nämnaren talet 6.
Är ett bråk större än ett annat?
Är bråket 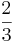 större än bråket
större än bråket 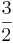 ? För att kunna avgöra detta måste vi först se till att de två bråken har samma nämnare; om de har samma nämnare behöver vi bara jämföra bråkens täljare för att avgöra vilket av de två bråken som är det största. Det finns ett automatiskt sätt att finna en gemensam nämnare:
? För att kunna avgöra detta måste vi först se till att de två bråken har samma nämnare; om de har samma nämnare behöver vi bara jämföra bråkens täljare för att avgöra vilket av de två bråken som är det största. Det finns ett automatiskt sätt att finna en gemensam nämnare:
-
- Bilda produkten av de enskilda bråkens nämnare.
I detta fall har vi två nämnare: talen 3 och 2. Deras produkt är talet 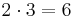 . För att bråket
. För att bråket 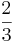 skall få en nämnare som är talet 6, måste vi multiplicera både täljaren och nämnaren med talet 2:
skall få en nämnare som är talet 6, måste vi multiplicera både täljaren och nämnaren med talet 2:
För att bråket 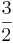 skall få en nämnare som är talet 6, måste vi multiplicera både täljaren och nämnaren med talet 3:
skall få en nämnare som är talet 6, måste vi multiplicera både täljaren och nämnaren med talet 3:
Nu behöver vi inte längre bekymra oss om nämnarna, utan vi kan koncentrera oss på att jämföra de två täljarna, 4 och 9. Vi ser att talet 4 är mindre än talet 9, vilket innebär att bråket  är mindre än bråket
är mindre än bråket 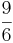 . Svaret på den ursprungliga frågan är därför Nej! bråket
. Svaret på den ursprungliga frågan är därför Nej! bråket 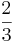 är inte större är bråket
är inte större är bråket 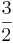 .
.
Bråk inom algebra
Ett bråk, inom algebran, är en kvantitet dividerat med en annan kvantitet. Om a och b är två tal så ges kvoten k av 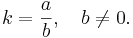 Ett annat skrivsätt är k = a/b. I äldre litteratur förekommer beteckningssättet a:b, och i engelskspråkig litteratur och på räknedosor används a÷b. Talet a benämns täljare och b nämnare.
Ett annat skrivsätt är k = a/b. I äldre litteratur förekommer beteckningssättet a:b, och i engelskspråkig litteratur och på räknedosor används a÷b. Talet a benämns täljare och b nämnare.
Allmänt
Om både täljaren och nämnaren är heltal, kan bråket betraktas som ett enskilt tal, och man säger då att talet är skrivet i bråkform, vilket i äldre språkbruk kallas allmänt bråk, och man gjorde då även följande distinktion: Om nämnaren är större än täljaren kallas bråket äkta eller egentligt . Om istället täljaren är större än nämnaren kallas bråket oäkta eller oegentligt.
Ett bråktal där täljaren är större än nämnaren kan också skrivas på blandad form (tidigare blandat tal): Exempel: 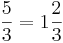 .
.
Ett bråk vars täljare är talet ett kallas stambråk.
Regler
Några regler för användningen av bråk:
- Man säger att man förkortar ett bråk när man kan förenkla bråket genom att dividera både täljaren och nämnaren med samma faktor. Exempelvis kan man förkorta 4╱6 med 2 och får då resultatet 2╱3 och x╱x2 med x och får 1╱x. Man bör dock vara försiktig med att förkorta med en algebraisk faktor som kan ha värdet noll, eftersom bråket inte är definierat om nämnaren är noll.
- Man säger att man förlänger ett bråk när man förändrar bråket genom att multiplicera både täljaren och nämnaren med samma faktor. Exempelvis kan man förlänga 2╱3 med 2 och får då resultatet 4╱6 och förlänga 1╱x med x och får x╱x2. Detta behövs till exempel vid addition och subtraktion av bråk, eftersom termerna då måste ha samma nämnare.
- Man kan addera bråk genom att omvandla varje term så att de har gemensam nämnare (göras liknämniga). Efter detta kan sedan täljarna adderas ihop. Ofta kan bråket förenklas efter additionen, men med minsta gemensamma nämnare fås många gånger den mest förenklade formen av bråket direkt.
- Bråk multipliceras genom att täljarna multipliceras för sig och nämnare multipliceras för sig. (Här behöver de inte först göras liknämniga.)
- Man dividerar två bråk genom att multiplicera täljarbråket med inverterade talet till nämnarbråket:

Decimaltal
Ett decimaltal (tidigare benämnt decimalbråk) är ett bråktal, vars nämnare är ett dekadiskt tal, det vill säga som skrivs med en etta följd av en eller flera nollor, till exempel 10, 100, 1 000, och så vidare. Ett alternativt skrivsätt för decimaltal är att använda decimaler:
- Bråken
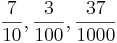 kan även skrivas på formeln 0,7; 0,03 eller 0,037.
kan även skrivas på formeln 0,7; 0,03 eller 0,037.
Periodiska decimaltal
Även periodiska decimaltal är bråktal, och kan förvandlas till bråkform eller blandad form:
(sätt a = 0,123123... så är 1 000a (= 123,123123... = 123 + 0,123123...) = 123 + a).
Generaliseringar
- Istället för tal a och b kan ett bråk bestå av kvoten mellan två polynom (ett sådant algebraiskt bråk kallas även rationellt uttryck).
- Inom abstrakt algebra sägs ovanstående regler vara gemensamt för godtyckliga kroppar. Om man startar med heltalsdomänen Q så kan alltid fältet som innehåller alla bråk av Q enkelt konstrueras.