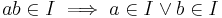Från Rilpedia

Ett primideal är inom matematik, specifikt ringteori, ett ideal I i en kommutativ ring R som uppfyller:

för alla a och b i R.

Exempel

• I ringen av heltal, 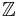, är ett primideal antingen nollidealet {0} eller på formen 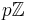(alla multiplar av p), där p är ett primtal.
• Alla maximala ideal är primideal. Det omvända gäller dock i allmänhet inte.

Egenskaper

• Om R är en kommutativ ring med etta och P är ett ideal i R är P ett primideal om och endast om kvotringen R/P är ett integritetsområde.
• Varje kommutativ ring med etta har minst ett primideal, en direkt följd av Krulls sats.
• Urbilden av ett primideal för en ringhomomorfi är ett primideal.