Haarmått
Från Rilpedia
Haarmått är ett mått i lokalt kompakta topologiska grupper så att det är volyminvariant. Till exempel är Lebesguemåttet Haarmåttet i  .
.
Innehåll |
Translation-invariant mått
Låt 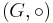 vara en grupp.
vara en grupp.
Om 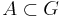 och
och 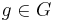 kallas mängden
kallas mängden
för vänstertranslationen för A och mängden
för högertranslationen för A.
En sigma-algebra 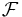 i
i 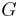 är vänstertranslationsinvariant om
är vänstertranslationsinvariant om
- för alla
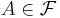 och
och 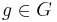 är
är 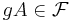 ,
,
likartat kan man definiera egenskapen att en sigmaalgebra är högertranslationsinvariant.
Om 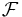 är en vänstertranslationsinvariant sigma-algebra så är måttet
är en vänstertranslationsinvariant sigma-algebra så är måttet ![\mu : \mathcal{F} \rightarrow [0,\infty]](/w/images/sv.rilpedia.org/math/d/2/c/d2c962abd3aff0fa5d3e04a80e210ca1.png) vänstertranslationsinvariant om
vänstertranslationsinvariant om
- för alla
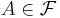 och
och 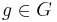 är
är 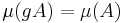 ,
,
likartat kan man definiera att ett mått är högertranslationsinvariant.
Haarmått
Låt 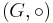 vara en lokalt kompakt topologisk grupp, dvs
vara en lokalt kompakt topologisk grupp, dvs
- paret
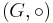 är en grupp,
är en grupp, - rummet
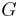 är ett lokalt kompakt topologiskt rum
är ett lokalt kompakt topologiskt rum - avbildningen
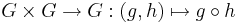 är kontinuerlig (i produkttopologin) och
är kontinuerlig (i produkttopologin) och - avbildningen
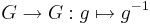 är kontinuerlig.
är kontinuerlig.
Då är Borelmängderna 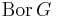 en vänster- och högertranslationsinvariant sigma-algebra.
en vänster- och högertranslationsinvariant sigma-algebra.
Det går att visa att det alltid finns (utan konstant) endast ett Radonmått
som är vänstertranslationsinvariant. Vi kallar detta mått vänster-Haarmåttet.
Man kan även visa att det alltid finns (utan konstant) endast ett Radonmått
som är vänster-translation-invariant som kallas höger-Haarmåttet.
Med utan konstant menas att Radonmåttet 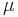 i
i 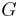 är vänstertranslationsinvariant om och endast om det finns
är vänstertranslationsinvariant om och endast om det finns 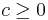 så att
så att 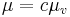 , likaså för det högertranslationsinvarianta måttet.
, likaså för det högertranslationsinvarianta måttet.
Det finns grupper 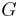 där
där 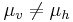 , men om
, men om
i 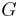 kallar vi måttet
kallar vi måttet
för Haarmåttet.
Egenskaper
- Om gruppen
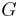 är en abelsk grupp så är
är en abelsk grupp så är 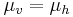 .
.
Exempel
- Rummet
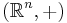 är en lokalt kompakt topologisk grupp med normtopologi. Dessutom är Lebesguemåttet över Borelmängder höger- och vänstertranslationsinvariant, dvs
är en lokalt kompakt topologisk grupp med normtopologi. Dessutom är Lebesguemåttet över Borelmängder höger- och vänstertranslationsinvariant, dvs
- för alla
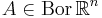 och
och 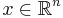 gäller att
gäller att 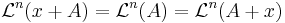 .
.
Så att Lebesguemåttet är Haarmåttet i  :
:
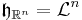 .
.
Detta innebär också att Lebesguemåttet är (utan konstant) det enda höger- och vänstertranslationsinvarianta måttet i  .
.
- Andra viktiga exempel för Haarmåttet är vridningsinvariant mått i ortogonalgruppen, dvs
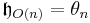 .
.
Referenser
- Paul Halmos (1950), Measure Theory, D. van Nostrand and Co.




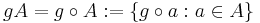
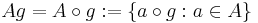
![\mu_v : \mbox{Bor} \, G \rightarrow [0,\infty]](/w/images/sv.rilpedia.org/math/2/f/6/2f635045c9efbe5aa31dc1a299f666c1.png)
![\mu_h : \mbox{Bor} \, G \rightarrow [0,\infty]](/w/images/sv.rilpedia.org/math/5/7/6/5764243019196cc90cbbd2e1c1e4d6eb.png)