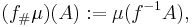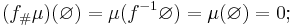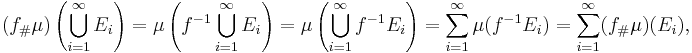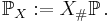Bildmått

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett bildmått är inom matematiken ett mått som avbildar en måttstruktur från andra måttrummet till andra.

Formell definition

Låt 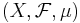(X,\mathcal{F},\mu) vara ett måttrum och 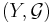(Y,\mathcal{G}) ett mätbart rum, dvs 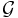\mathcal{G} är en sigma-algebra i Y. Om 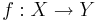f : X \rightarrow Y är en mätbar funktion så är µ:s f-bildmåttet eller bildmåttet en funktion f_\#\mu : \mathcal{G} \rightarrow [0,\infty] definierad som:

(f_\#\mu)(A) := \mu (f^{-1} A),

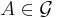för A \in \mathcal{G}, dvs man mäta urbilder med måttet µ.

Med urbildens egenskaper man kan visa nästan:

(f_\#\mu)(\varnothing) = \mu (f^{-1} \varnothing) = \mu(\varnothing) = 0;
  • Bildmåttet är σ-additiv, dvs om E1, E2, E3, ... är en uppräknelig sekvens av parvis disjunkta mängder i 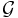\mathcal{G} så är
(f_\#\mu)\left(\bigcup_{i=1}^\infty E_i\right) = \mu \left(f^{-1} \bigcup_{i=1}^\infty E_i\right) = \mu \left(\bigcup_{i=1}^\infty f^{-1} E_i\right) = \sum_{i=1}^\infty \mu(f^{-1} E_i) = \sum_{i=1}^\infty (f_\#\mu)(E_i),

eftersom f-1E1, f-1E2, f-1E3, ... är en uppräknelig sekvens av parvis disjunkta mängder i 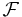\mathcal{F}.

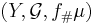Dvs bildmåttet är ett mått \mathcal{G} \rightarrow [0,\infty]. Så att (Y,\mathcal{G},f_\# \mu) är ett måttrum.

Sannolikhetsfördelning

Huvudartikel: Sannolikhetsfördelning

En viktig tillämpning för bildmåttet är stokastisk variabels fördelning. Mer precist, låt 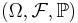(\Omega,\mathcal{F},\mathbb{P}) vara ett sannolikhetsrum och 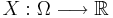X : \Omega \longrightarrow \R en stokastisk variabel. Så att sannolikhetsfördelning för X är ett bildmått

\mathbb{P}_X := X_\# \mathbb{P}\, .

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Bildm%C3%A5tt"
Personliga verktyg