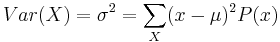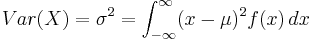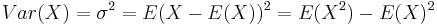Varians

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Varians är ett begrepp inom matematisk statistik. Det är exempel på spridningsmått för en sannolikhetsfördelning, det vill säga ett mått på hur utspridd fördelningen är kring väntevärdet (μ). Liksom väntevärdet, är varians en egenskap hos en stokastisk variabel X och dennas

sannolikhetsfördelning.

Matematiskt definieras variansen σ2 för en diskret sannolikhetsfördelning som

Var(X) = \sigma^2 = \sum_{X}^{} (x-\mu)^{2}P(x)

där summeringen görs över alla x i utfallsrummet Ω och μ är väntevärdet på X.
För en kontinuerlig sannolikhetsfördelning definieras variansen som

Var(X) = \sigma^2 = \int_{-\infty}^{\infty} (x-\mu)^{2}f(x)\,dx

där f(x) är fördelningens täthetsfunktion (frekvensfunktion). Man kan också definiera variansen med hjälp av begreppet väntevärde (E(X)):

\displaystyle Var(X) = \sigma^2 = E(X-E(X))^2 = E(X^2) - E(X)^2

det vill säga kvadraten på väntevärdet för avvikelsen från väntevärdet.

Kvadratroten ur variansen (σ) kallas för sannolikhetsfördelningens standardavvikelse. Standardavvikelsen är, likt varians, exempel på spridningsmått för en sannolikhetsfördelning.

Hämtad från "https://sv.rilpedia.org/wiki/Varians"
Personliga verktyg