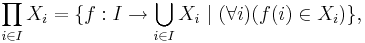Urvalsaxiomet
Från Rilpedia
Urvalsaxiomet är ett mängdteoretiskt axiom som förr var kontroversiellt (och som till viss del är det fortfarande). Som beteckning för urvalsaxiomet används den väletablerade förkortningen AC (bokstäverna står för engelska "Axiom of Choice"). En mängdteori (axiomuppsättning) som inkluderar AC sägs vara en teori "med urval".
AC säger att om vi har en mängd av icke-tomma mängder så finns det en funktion, den sk urvalsfunktionen, som väljer ut ett element ur var och en av dessa. Med andra ord, låt 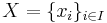 vara en godtycklig mängd av icke-tomma mängder. Då gäller att:
vara en godtycklig mängd av icke-tomma mängder. Då gäller att:
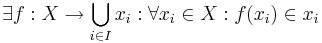
En ofta använd formulering är även att en godtycklig kartesisk produkt av icke-tomma mängder är icke-tom. Att dessa båda formuleringar är ekvivalenta fås genom definitionen av den kartesiska produkten för oändliga produkter:
Existensen av en urvalsfunktion är alltså ekvivalent med att det finns en funktion f i mängden som definierar den kartesiska produkten.
I en modifierad form av urvalsaxiomet, det uppräkneliga urvalsaxiomet, är I begränsad till att vara uppräknelig.
Problemet med AC är att det inte är så enkelt som övriga axiom i Zermelo-Fraenkels mängdteori (ZF). Ändå tycks AC vara nödvändigt för att bevisa en massa saker som borde vara sanna men som inte följer ur endast ZF.
AC följer alltså inte av axiomen i ZF, så därför bildade man en ny mängdteori, ZFC (Zermelo-Fraenkels mängdteori med urval).
Några kopplingar mellan AC och andra satser:
- AC är ekvivalent med välordningssatsen.
- AC är ekvivalent med Zorns lemma.
- AC är ekvivalent med påståendet att α = α2, för varje oändligt kardinaltal α.
- AC implicerar Tarski-Banachs paradox.
- AC impliceras av Löwenheim-Skolem-Tarskis sats.
- AC är ekvivalent med Tychonoffs sats.
- AC är ekvivalent med påståendet "varje vektorrum har en bas".