Symmetrisk matris

Texten från svenska Wikipedia

En symmetrisk matris M har egenskapen att den är identisk med sin transponatmatris.

Alltså, matrisen M är symmetrisk omm

$M = M T$ .

Härav följer också att M måste vara kvadratisk.

Ex 1:

Låt

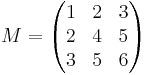
$M = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 6 \end{pmatrix}$

Eftersom

$M T = M$

så är M symmetrisk.

Ex 2:

Låt

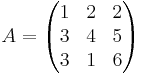
$A = \begin{pmatrix} 1 & 2 & 2 \\ 3 & 4 & 5 \\ 3 & 1 & 6 \end{pmatrix}$

Då är

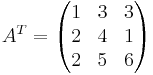
$A^T = \begin{pmatrix} 1 & 3 & 3 \\ 2 & 4 & 1 \\ 2 & 5 & 6 \end{pmatrix}$

vilket ju inte är lika med A. Alltså är A inte en symmetrisk matris.

Ex 3:

Visa att för varje reell matris A så är matrisen $A T A$ symmetrisk, förutsatt att matrismultiplikationen är tillåten.

Lösn.:

Med transponatreglerna ser vi att

$(A T A) T = (A) T (A T) T = A T A$

vilket ju är samma sak. Alltså är $A T A$ alltid symmetrisk förutsatt att multiplikationen är tillåten.

Du kan nu säkert visa själv att om multiplikationen inte är tillåten så är istället $A A T$ alltid symmetrisk.

Se även