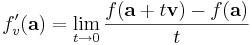Riktningsderivata

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom matematik, särskilt flervariabelanalys, är riktningsderivata ett mått på hur snabbt en funktion förändras i en viss riktning. Givet en reellvärd funktion f, en punkt a och en linje x = a + tv där v är en enhetsvektor, ges riktningsderivatan i riktningen v av

f'_v(\mathbf{a}) = \lim_{t \to 0} \frac{f(\mathbf{a} + t\mathbf{v}) - f(\mathbf{a})}{t}

Med hjälp av gradienten kan riktningsderivatan även uttryckas på den mer praktiska formen

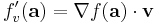f'_v(\mathbf{a}) = \nabla f(\mathbf{a}) \cdot \mathbf{v}.

Riktningsderivatan utgör en generalisering till godtyckliga riktningar av den partiella derivatan, som fås då v sätts lika med en basvektor.

Hämtad från "https://sv.rilpedia.org/wiki/Riktningsderivata"
Personliga verktyg