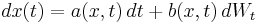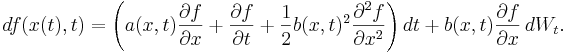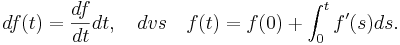Itōs lemma
Från Rilpedia
Itōs lemma (Itōs formel) är ett berömt resultat inom den gren av matematiken som kallas stokastisk analys (stokastisk kalkyl). Det är upkallat efter Kiyoshi Ito.
Den utgör en av de tre fundamentala resultaten på vilka teorin för stokastisk analys är konstruerad:
- Den kvadratiska variationsprocessen för Wienerprocessen.
- Konstruktionerna av begreppet stokastisk integral.
- Itōs lemma.
Kvadratisk variation hos Wienerprocessen
Det faktum att Wienerprocessens vägar är av oändlig variation medför att begreppet stokastisk integral inte kan definieras på samma sätt som exempelvis Lebesgue-Stieltjesintegralen.
Konstruktion av stokastisk integral
Stokastiska integraler konstrueras därför som objekt som existerar i L2-rum. (Se funktionalanalys.) Detta får som konsekvens att man inte kan tolka en stokastisk integral som arean under grafen för en stokastisk process.
Det finns lika många olika konstruktioner av begreppet stokastisk integral som det finns reella tal. Den mest använda av dessa konstruktioner är Itōs konstruktion. En annan konstruktion, som används främst då man studerar stokastiska differentialekvationer på differentiabla mångfalder, är den som har fått namn efter Stratonovich.
Itōs lemma
Antag att x(t) är en Itōprocess, det vill säga det är en stokastisk process som är en lösning till den stokastiska differentialekvationen
där W är en Wienerprocess, och f(x, t) är en funktion med kontinuerliga andraderivator.
Då är f(x(t),t) också en Itōprocess och den löser den stokastiska differentialekvationen
Itōs lemma innehåller analysens fundamentalsats som ett specialfall: Om man väljer funktionerna b = 0, a = 1 och funktionen f till att endast bero på argumentet t, så reduceras Itōs lemma till
På samma sätt som analysens fundamentalsats är grundläggande för ämnet matematisk analys, är Itōs lemma grundläggande för stokastisk analys.