Gaussiska heltal
Från Rilpedia
Ett gaussiskt heltal eller gausskt heltal är ett komplext tal z som kan skrivas på formen
- z = x + iy,
där  , d. v. s. x och y är vanliga (reella) heltal. Exempelvis är 2+3i, 4-8i och 19 gaussiska heltal (eftersom de också kan skrivas som 2+i·3, 4+i·(-8) respektive 19+i·0). Summor, differenser och produkter av gaussiska heltal är också gaussiska heltal:
, d. v. s. x och y är vanliga (reella) heltal. Exempelvis är 2+3i, 4-8i och 19 gaussiska heltal (eftersom de också kan skrivas som 2+i·3, 4+i·(-8) respektive 19+i·0). Summor, differenser och produkter av gaussiska heltal är också gaussiska heltal:
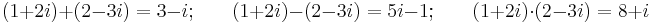 .
.
Vidare finns en heltalsvärd norm v definierad genom v(x + iy) = x2 + y2, och en "division med kvot och rest": Om a och b är två gaussiska heltal, och 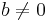 , så finns två gaussiska heltal q och r, sådana att a = qb + r och
, så finns två gaussiska heltal q och r, sådana att a = qb + r och 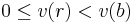 . (q kan bildas genom att man var för sig avrundar realdelen och imaginärdelen av det komplexa talet
. (q kan bildas genom att man var för sig avrundar realdelen och imaginärdelen av det komplexa talet 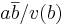 till närmaste heltal.) Mängden av alla gaussiska heltal utgör därför en euklidisk domän.
till närmaste heltal.) Mängden av alla gaussiska heltal utgör därför en euklidisk domän.



