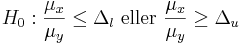Bioekvivalens
Från Rilpedia
| Den här artikeln behöver språkvård. Hjälp till genom att förbättra texten. Se Rilpedia:Korrekturläsning för mer information, och Kategori:Rilpedia:Språkvård för fler artiklar i behov av språkvård. |
| Den här artikeln anses vara otydlig eller onödigt fackspråklig. Hjälp gärna till att förtydliga artikeln och göra den mer lättläst. Se eventuellt diskussionssidan för mer information. |
Bioekvivalens är ett begrepp inom farmakokinetik som används för att beskriva en likvärdig effekt in vivo av två olika läkemedel, vanligtvis med olika tillverkare, baserade på samma aktiva substans. Om de två läkemedlen konstateras vara bioekvivalenta, kan de två läkemedlen betraktas som ett och samma samma. Detta är inte minst aktuellt i samband med generiska läkemedel, där det är viktigt att veta om "kopian" beter sig på samma sätt som det ursprungliga läkemedlet.
Testning för bioekvivalens
Ett alternativ till t-testet (som inom läkemedelsindustrin används för att testa om två mediciner har samma effekt) är ekvivalenstest. Givet två utfall som skall jämföras – till exempel där två likvärdiga mediciner ger samma effekt, men den ena är billigare att tillverka – ställs följande nollhypotes upp:
I dagsläget används inom läkemedelsindustrin 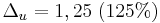 respektive
respektive 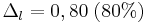
Man vill alltså landa i alternativhypotesen att kvoten mellan μx och μy ligger i intervallet 0,8–1,25.
Genom att logaritmera får man 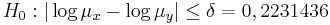
To test the hypothesis H0 on significance level α we construct  confidence intervals with the endpoints
confidence intervals with the endpoints 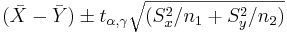
där Sx och Sy är den skattade stickprovsvariansen. Antalet frihetsgrader γ fås ur följande formel ![\gamma= \left\lfloor\frac{(S_1^2/n_1+S_2^2/n_2)^2}{\frac{[S_1^2/n_1]^2}{n_1-1}+\frac{[S_2^2/n_2]^2}{n_2-1}}\right\rfloor](/w/images/sv.rilpedia.org/math/8/2/0/8202bfac812a9773f6dd0a7d6396b7ab.png)
Externa länkar
- Sjukhusläkaren och Sjukhusläkarföreningen – Sjukhusläkaren reder ut generika-begreppen