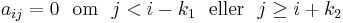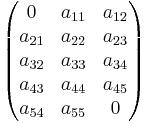Bandmatris
Från Rilpedia
En bandmatris är inom matematik en gles matris sådan att endast elementen i ett band runt huvuddiagonalen är nollskilda; bandet utgörs av ett antal diagonaler ovanför respektive nedanför huvuddiagonalen.
Mer strikt uttryckt kan man säga att för en n×n-bandmatris med elementen aij ska det finnas två positiva heltal k1 och k2 så att
k1 brukar kallas vänsterbandbredd och k2 för högerbandbredd. Bandbredden för matrisen är antalet diagonaler där det finns nollskillda element, k1 + k2 + 1.
Specialfall inträffar då k1 = k2 = 0 då man får en diagonalmatris, då k1 = k2 = 1 då man får en tridiagonal matris, och då k1 = 0 och k2 = n − 1 då man får en nedåt triangulär matris. En uppåt triangulär matris fås om k1 = n − 1 och k2 = 0.
Tillämpningar
Inom beräkningsvetenskap fås ofta bandmatriser vid användning av finita elementmetoden.
Lagring
Då bandmatriser innehåller mest nollor kan man i datorprogram spara lagringsutrymme om man endast lagrar bandet, exempelvis kan en 5 × 5-tridiagonal matris
lagras som en 5 × 3-matris