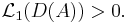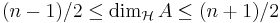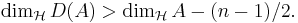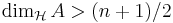Avståndsmängd
Från Rilpedia
Avståndsmängd är ett begrepp inom matematik. Avståndsmängden för en delmängd till ett metriskt rum är mängden av alla avstånd mellan element mängden.
Innehåll |
Formell definition
Låt 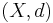 vara ett metriskt rum och
vara ett metriskt rum och 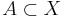 en mängd. Då är avståndsmängden för mängden
en mängd. Då är avståndsmängden för mängden 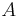 mängden
mängden
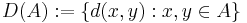 ,
,
dvs samlingen av alla avstånd i 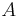 .
.
Tillämpningar
En viktig tillämpning för avståndsmängden är diametern, diam, av en mängd som är supremum för avståndsmängden. Mer precist, diametern för en mängd 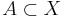 är talet
är talet
Egenskaper
Eftersom 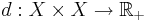 är en metrik så är
är en metrik så är
och
för alla 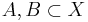 där
där 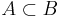 .
.
Geometri
En intressant fråga är att givet att man vet någonting om mängdens geometri kan man veta det även för avståndsmängdens geometri? I 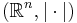 finns några samband.
finns några samband.
Mått
Steinhaus sats säger att om 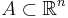 är Lebesguemätbar och den har ett positivt n-dimensionellt Lebesguemått
är Lebesguemätbar och den har ett positivt n-dimensionellt Lebesguemått 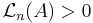 , så är 1-dimensionella Lebesguemåttet för avståndsmängden positiv, dvs
, så är 1-dimensionella Lebesguemåttet för avståndsmängden positiv, dvs
Dimension
Det också finns några satser för dimension av avståndsmängder. Låt 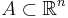 vara en Borelmängd.
vara en Borelmängd.
- så är
- Om Hausdorffdimensionen
- så kan man också säga någonting om Lebesguemåttet:
- Detta innebär
Se även
Referenser
- Mattila, P. Geometry of sets and measures in euclidean spaces: fractals and rectifiability, Cambridge University Press, 1995.




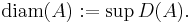
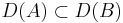
![D(A) \subset [0,\mathrm{diam}(A)]\,](/w/images/sv.rilpedia.org/math/8/e/4/8e4ecb80f2808689f7d88ab90d49a1d4.png)