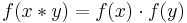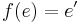Monoid

Från Rilpedia

Texten från svenska Wikipedia

En monoid är inom abstrakt algebra ett par (M, * ) (ofta säger man bara M och menar hela monoiden), där M är en mängd och * är en binär operator på M, vilken lyder följande regler:

• stängdhet: för alla a,b i M, är a * b i M (detta följer egentligen direkt ur att * är en binär operator, och behöver inte specificeras separat)
• neutralt element: det finns ett element e i M, så att för alla a i M, a * e = e * a = a.
• associativitet: * är en associativ operator; det vill säga, (a * b) * c = a * (b * c) för alla a,b,c i M.

Med andra ord är en monoid en semigrupp med ett neutralt element.

En kommutativ monoid eller abelsk monoid är en monoid där operatorn även är kommutativ, dvs:

• a * b = b * a för alla a,b i M.

(D, * ) sägs vara en submonoid till en monoid (M, * ) om D är en delmängd till M, D innehåller det neutrala elementet och för alla a,b i K så ligger även a * b i K. (D, * ) är då även monoid i sig själv.

Exempel

Naturliga talen

De naturliga talen, 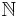, med additionsoperatorn + bildar en abelsk monoid 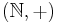med det neutrala elementet 0.

Man kan också bilda en monoid med multiplikationsoperatorn 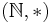, som även den är abelsk, med det neutrala elementet 1.

Strängar

Mängden av alla ändliga strängar över ett alfabet bildar en monoid med konkatenering som operator och den tomma strängen som neutralt element.

Monoidhomomorfier

En homomorfi mellan två monoider, 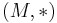och 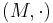, är en funktion 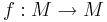som upppfyller:

där e och e' är neutrala element för 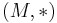respektive .

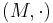Om en monoidhomomorfi är bijektiv kallas den för isomorfi, och två monoider som har en monoidisomorfi mellan sig kallas isomorfa.

Se även