Leopold Kronecker
Från Rilpedia
 |
|
| Född: | 7 december 1823 Liegnitz, Preussen |
| Död: | 29 december, 1891 Berlin, Tyskland |
| Nationalitet: | Preussisk |
| Forskningsområde: | Matematik |
| Institutioner: | Berlins universitet |
| Alma mater: | Berlins universitet |
| Akademisk handledare: | Johann Encke Gustav Dirichlet |
| Nämnvärda studenter: | Georg Cantor Kurt Hensel Adolf Kneser Mathias Lerch Franz Mertens |
| Känd för: | Kroneckerdelta Kroneckerprodukt Kroneckers sats Kroneckers lemma |
Leopold Kronecker, född 7 december 1823 i Liegnitz, död 29 december 1891 i Berlin, tysk matematiker.
Kronecker blev student i Berlin 1841, där han var en av Dirichlets förnämsta elever, och promoverades till filosofie doktor 1845. 1861 började han i Berlin hålla enskilda föreläsningar i matematik och blev 1883 professor i matematik vid Humboldt-Universität zu Berlin i staden.
Som vetenskaplig författare utvecklade Kronecker en ganska stor produktivitet. Utgångspunkten för denna hans verksamhet utgjordes av undersökningar rörande formen för rötterna till en algebraisk ekvation, som kan lösas medelst radikaler, varvid Kronecker fullföljde den tankegång, som ledde den norske matematikern Abel och fransmannen Galois vid deras banbrytande forskningar på detta område. Senare ägnade Kronecker en mängd avhandlingar åt högre algebra och åt talteori samt särskilt åt sådana frågor, som samtidigt berör dessa båda grenar av matematiken. Bland speciella ämnen, som han behandlade, må nämnas teorin för kvadratiska former, komplex multiplikation av elliptiska funktioner, Sturms funktioner och karakteristikteori, i sammanhang varmed han generaliserade den så kallade Cauchys integralsats till att gälla även om funktioner av flera oberoende variabler. I avlägsnare förbindelse med hans övriga arbeten står hans lösning av femtegradsekvationer, vilken han upptäckte ungefär samtidigt med Hermite och Brioschi samt sedermera i flera avhandlingar ytterligare förbättrade och utvecklade.
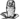Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, Kronecker, 1904–1926 (Not).
