Elliptisk funktion

Från Rilpedia

Texten från svenska Wikipedia

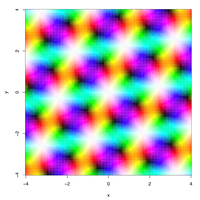
Elliptiska funktioner, mat., är funktioner, definierade på det komplexa talplanet, som är periodiska i två riktningar. Det kan jämföras med vanliga trigonometriska funktioner som sinus och cosinus, vilka är periodiska i en riktning med perioden $2π$ radianer. Elliptiska funktioner är inverser till elliptiska integraler, som kommer ur problemet att beräkna båglängden på ellipser.

En funktion som är dubbelperiodisk och analytisk utom i sina poler är en elliptisk funktion. Formellt sett är en dubbel-periodisk funktion en funktion som uppfyller följande ekvation: 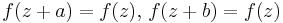$f(z + a) = f(z),\,f(z + b) = f(z)$

där a och b då är funktionens perioder.

Teorien för de elliptiska funktionerna är till sin väsentligaste del utvecklad av Niels Henrik Abel, Karl Weierstrass och Carl Gustav Jakob Jacobi.

Innehåll

1 Definitioner
2 Viktiga egenskaper hos elliptiska funktioner
3 Konstruktion
4 Referenser

Definitioner

En tal w som upfyller sambandet att $f (z + w) = f (z)$ kallas för en period till f.

Ett användbart begrepp för att beskriva elliptiska funktioner är fundamentalparallellogrammet. Det konstrueras via funktionens period. Om de två perioderna a och b är sådana att man kan beskriva alla andra perioder w som $w = m a + n b$ där m och n är heltal, så kallas a och b för fundamentala perioder för f. Om man i tur och ordning förbinder punkterna 0, a, a+b och b med linjer får vi ett fundamental-parallellogram. I varje sådant parallellogram kommer funktionen att bete sig på exakt samma sätt, på grund av periodiciteten. Alltså behöver vi bara titta på ett fundamentalparallellogram då vi studerar funktionen. Ett sådant parallellogram kan också förskjutas med heltals-multipler av a och b. Ibland är det mer användbart att ha ett parallellogram där det inte finns några poler längs kanterna. Periodiciteten tillåter att vi flyttar parallellogrammet, utan att rotera det, tills vi får ett parallellogram med de önskade egenskaperna. Det kallas då en cell.

Viktiga egenskaper hos elliptiska funktioner

Antalet poler i en cell är ändligt

Om inte, skulle polerna ha ett gränsvärde, enligt den tvådimensionella motsvarigheten till Bolzanos teorem^{[källa behövs]}. Detta gränsvärde skulle då vara en väsentlig singularitet, och funktionen är då enligt definitionen inte en elliptisk funktion.

Antalet nollställen i en cell är ändligt

Om inte, så skulle funktionens invers ha ett oändligt antal poler, och därför ha en väsentlig singularitet enligt ovan. Denna singularitet skulle också vara en singularitet hos originalfunktionen, som därför inte skulle vara elliptisk. (Detta argument förutsätter dock att funktionen inte är konstant noll.)

En elliptisk funktion f(z) som saknar poler i en cell är konstant

Om f(z) inte har några poler inuti en cell så är den analytisk enligt definitionen av elliptisk funktion. Av det följer att den är begränsad i och på gränsen av cellen. Det finns alltså ett tal K sådant att 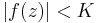$\left| f(z) \right| < K$ då z ligger i eller på gränsen av cellen. Av de periodiska egenskaperna för funktionen följer att om detta gäller för alla z i en cell, så gäller det för alla z. Detta ger, enligt Liouvilles sats, att funktionen är konstant.

Summan av residyerna vid polerna i en cell för en elliptisk funktion är noll.

Låt C vara konturen som bildas av kanterna på cellen, och låt hörnen på cellen vara

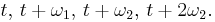$t,\,t + \omega_1,\,t+\omega_2,\,t+2\omega_2.$ Summan av residyerna av f(z) vid dess poler inuti C är då

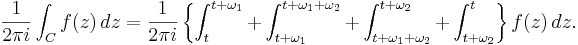
$\frac{1}{2 \pi i} \int_{C} f(z)\, dz = \frac{1}{2 \pi i} \left\{ \int_{t}^{t + \omega_1} + \int_{t + \omega_1}^{t + \omega_1+ \omega_2}+\int_{t + \omega_1+ \omega_2}^{t + \omega_2} + \int_{t + \omega_2}^{t } \right\} f(z) \, dz.$

Om man i intervallen två och tre skriver z som $z + ω 1$ respektive $z + ω 2$ blir högerledet

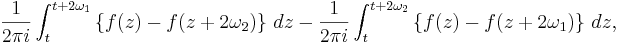
$\frac{1}{2\pi i} \int_{t}^{t+2\omega_1} \left\{ f(z)-f(z+2\omega_2) \right\} \, dz - \frac {1}{2\pi i} \int_{t}^{t+2\omega_2} \left\{ f(z)-f(z+2\omega_1) \right\} \,dz,$

och både dessa integraler försvinner på grund av periodiciteten hos f(z). Alltså är 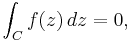$\int_{C} f(z)\,dz=0,$ och satsen visad.

Gradtalet hos en elliptisk funktion

Gradtalet hos en elliptisk funktion är lika med antalet lösningar i en cell till ekvationen $f (z) = c$ Detta tal beror bara på funktionen och inte på talet c, och är dessutom lika med antalet poler i cellen. Detta kan visas på följande sätt: Skillnaden mellan antalet nollställen och antalet poler hos f(z) - c i en cell kan skrivas som

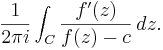
$\frac {1}{2\pi i} \int_{C} \frac {f'(z)}{f(z)-c}\, dz.$

Eftersom

$f'(z + ω 1) = f'(z + ω 2) = f'(z),$

så kan man genom att dela konturen i fyra bitar på samma sätt som ovan visa att dess värde är noll. Det ger att antalet nollställen till f(z) - c är lika med antalet poler hos f(z) - c. Men en pol hos f(z) - c är en pol också hos f(z) och tvärtom. Det ger att antalet nollställen hos f(z) - c är lika med antalet poler hos f(z), och detta antal är oberoende av c.

Gradtalet hos en elliptisk funktion är alltid minst 2. Skulle gradtalet vara 1 skulle det motsvara en funktion med en enda pol, och den skulle då ha en residy skild från 0, vilket motsäger satsen att residyn alltid skall vara noll.

De enklaste elliptiska funktionerna är alltså de av grad två. De kan delas in i två grupper. Den första innehåller de som har två enkla poler med residyer av motsatta tecken, och den andra som har en enda dubbel pol. Ett exempel på en funktion i den andra gruppen är Weierstrass funktion 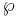$\wp$ som beskrivs längre ned. Det går att visa att alla elliptiska funktioner går att skriva i termer av funktionen ur endera gruppen.

Derivatan av en elliptisk funktion är också en elliptisk funktion, med samma perioder.

Konstruktion

$\wp$ definierad på en del av det komplexa planet. I bilden motsvarar vitt en pol och svart ett nollställe. Man kan se det regelbundna mönstret av poler.

Funktionen 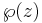$\wp(z)$ introducerads av Weierstrass. Den kan användas för att konstruera alla andra elliptiska funktioner. Den kan definieras som följande funktion: 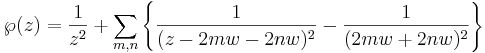$\wp(z)= \frac {1}{z^2} + \sum_{m, n} \left\{ \frac {1}{(z - 2mw - 2nw)^2} - \frac {1}{(2mw + 2nw)^2} \right\}$ där

∑

m,n

är summan av funktionen för alla heltalsvärden på m och n.

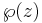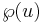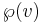Funktionen $\wp(z)$ uppfyller också vad som kallas för ett additions-teorem. Det betyder att funktionens värde för u+v kan uttryckas med hjälp av $\wp(u)$ och $\wp(v)$ . Alltså gäller att

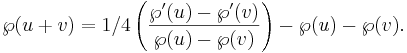
$\wp(u+v) = 1/4 \left( \frac{\wp'(u) - \wp'(v) }{\wp(u)-\wp(v)} \right) - \wp(u) - \wp(v).$

Referenser

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (Se kapitel 16.)
Naum Illyich Akhiezer, Elements of the Theory of Elliptic Functions, (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
Tom M. Apostol, Modular Functions and Dirichlet Series in Number Theory, Springer-Verlag, New York, 1976. ISBN 0-387-97127-0 (Se kapitel 1.)
Albert Eagle, The elliptic functions as they should be. Galloway and Porter, Cambridge, England 1958.
E. T. Whittaker and G. N. Watson. A course of modern analysis, Cambridge University Press, 1952

Elliptisk funktion

Från Rilpedia

Innehåll

Definitioner

Viktiga egenskaper hos elliptiska funktioner

Konstruktion

Referenser

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk